Hallo,
a) Begründe, dass der Graph von f maximal drei Extremstellen besitzt.
Extremmstellen sind Nullstellen der 1. Ableitung. Die 1. Ableitung dieser Funktion hat den Grad 3 und kann daher maximal 3 Nullstellen besitzen.
Bevor ich weiter rechne, überprüfe bitte mal die Funktionsgleichung, die du geschrieben hast. Ist die so richtig?
\(f(x)=-\frac{1}{10}x^4+\frac{4}{9375}x^3-\frac{13}{250}x^2+\frac{8}{5}x+140\)
Gruß, Silvia
\(f(x)=-\frac{1}{10^6}x^4+\frac{4}{9375}x^3-\frac{13}{250}x^2+\frac{8}{5}x+140\)
b) Berechne die Koordinaten der Extrempunkte des Graphen von f und bestimme die Art der Extrempunkte.
Bilde die 1. Ableitung, setze sie = 0 und löse nach x auf.
Setze deine Ergebnisse dann in die 2. Ableitung ein um zu prüfen, ob es sich um Hoch- oder Tiefpunkte handelt. Die y-Koordinaten der Punkte bestimmst du, indem du deine Ergebnisse in f(x) einsetzt.
c) Der Graph von schließt mit den Koordinatenachsen und der zur y-Achse parallelen Geraden mit der Gleichung x = 240 ein Flächenstück ein.
1. Schraffiere das Flächenstück in der nachfolgenden Abbildung.
Das könnte so aussehen:
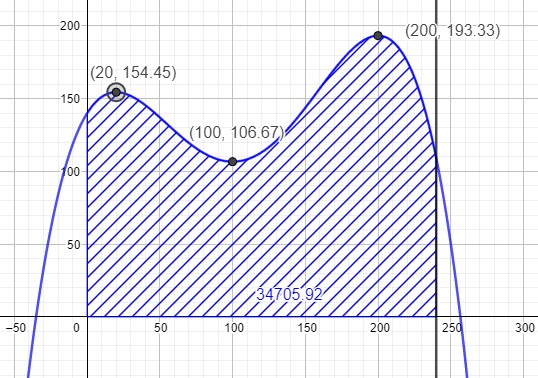
2. Bestimme den Flächeninhalt des Flächenstücks.
Berechne das \(\int \limits_{0}^{240}f(x)\; dx\)