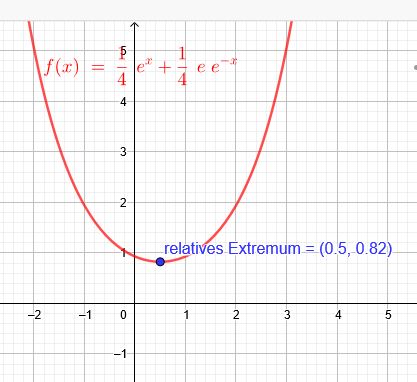
"Wie muss a gewählt werden, wenn das relative Extremum von \(f_a(x)=\frac{1}{4}*e^{x}+a*e^{-x}\) an der Stelle \(x=0,5\) liegen soll?"
\(f_a´(x)=\frac{1}{4}*e^{x}+a*e^{-x}*(-1)=\frac{1}{4}*e^{x}-a*e^{-x}\)
\(f_a´(0,5)=\frac{1}{4}*e^{0,5}-a*e^{-0,5}=0\)
\(a*e^{-0,5}=\frac{1}{4}*e^{0,5} |:e^{-0,5}\)
\(a=\frac{1}{4}* \frac{e^{0,5} }{e^{-0,5}} =\frac{1}{4}* e^{0,5}*e^{0,5}=\frac{1}{4}* e\)