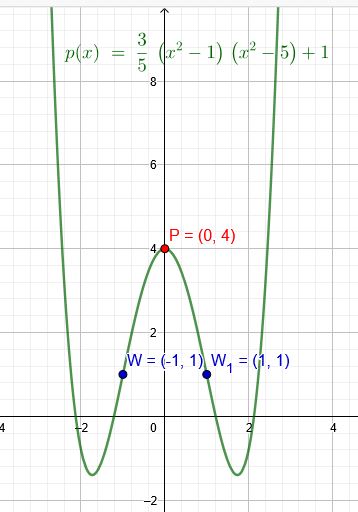
"Der Graph einer ganzrationalen Funktion vierten Grades ist achsensymmetrisch zur y- Achse und schneidet diesen im Punkt \(P(0|4)\). Im Punkt \(W(-1|1)\) hat der Graph einen Wendepunkt."
Ich verschiebe den Graph um 1 Einheit nach unten:
\(P(0|4)\)→\(P´(0|3)\)
\(W(-1|1)\)→\(W´(-1|0)\) Wegen der Achsensymmetrie gilt zudem \(W_1´(1|0)\)
\(f(x)=a*(x+1)*(x-1)*(x^2-N^2)=a*(x^2-1)*(x^2-N^2)\)
\(P´(0|3)\)
\(f(0)=a*(0-1)*(0-N^2)=a*N^2=3\) →\(a=\frac{3}{N^2}\)
\(f(x)=\frac{3}{N^2}*[(x^2-1)*(x^2-N^2)]\)
\(f´(x)=\frac{3}{N^2}*[2x*(x^2-N^2)+(x^2-1)*2x]=\frac{3}{N^2}*[4x^3-2x*N^2-2x]\)
\(f´´(x)=\frac{3}{N^2}*[12x^2-2*N^2-2]\)
\(f´´(1)=\frac{3}{N^2}*[12-2*N^2-2]=0\) → \(N^2=5\) \(a=\frac{3}{5}\)
\(f(x)=\frac{3}{5}*(x^2-1)*(x^2-5)\)
Nun wieder 1 Einheit nach oben:
\(p(x)=\frac{3}{5}*(x^2-1)*(x^2-5)+1\)