Berechnen Sie die Seillänge

Question

Aufgabe:

EIn 20 Meter hoher Ballon wird durch Tangentiale Seile gehalten. Diese sind in A(-6/18) und B (6/18) befestigt. Berechnen Sie die Seillänge

Problem/Ansatz:

Mein Ansatz wäre, den Mittelpunkt zu berechnen und eine Gerade von Mittelpunkt zu zB B aufzustellen. Diese müsste dann senkrecht? zu der Geraden von B zu der Befestigung am Boden sein und somit könnte ich die gesuchte gerade aufstellen. Ich denke aber nicht, dass es richtig ist.

Comments

Ich denke aber nicht, dass es richtig ist.

Ich schon.

Answer 1

Hallo,

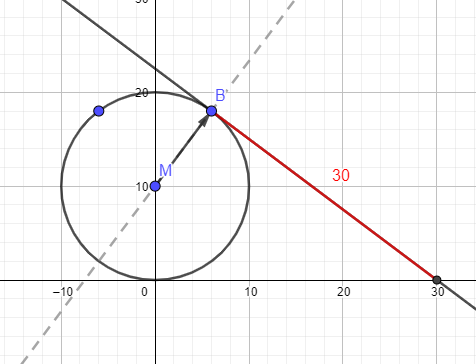
die Tangenten stehen senkrecht zu den Geraden durch den Mittelpunkt und A bzw. B. Ich rechne mit dem Punkt B.

Gerade durch MB

$g:\;\vec{x}=\begin{pmatrix} 0\\10 \end{pmatrix}+r\cdot \begin{pmatrix} 6\\8 \end{pmatrix}$

Wenn du die Koordinaten des Richtungsvektors vertauschst und einmal das Vorzeichen wechselst, erhältst du den Richtungsvektor der Tangente, B der Ortsvektor.

$t:\;\vec{x}=\begin{pmatrix} 6\\18 \end{pmatrix}+s\cdot \begin{pmatrix} 8\\-6 \end{pmatrix}$

Wandle diese Gleichung in die allgemeine Form y = mx + b um.

$t=-\frac{3}{4}x+22,5$

Berechne die Nullstelle und anschließend den Abstand von dieser bis zu B.

Gruß, Silvia

Comments

Warum macht ihr die Sache nicht so einfach wie sie in Wirklichkeit ist ?

Die Dreiecke sind ähnlich !

---

Da die Aufgabe offenbar mit Vektoren gelöst werden soll, wollte ich nicht auf diese simple Methode hinweisen ;-)

---

Die Dreiecke sind ähnlich !

Wohl kaum. Die Farben unterscheiden sich sehr deutlich.

---

Du hast ja offensichtlich überhaupt keine blasse Ahnung vom Ähnlichkeitsbegriff.

---

@Silvia:

... wollte ich nicht auf diese simple Methode hinweisen ;-)

Die Worte les' ich wohl, allein mir fehlt der Glaube :-)

Answer 2

siehe Skizze Sylvia ( grün )
r = 10 m
x = 6 m
Steigungswinkel
cos alpha = 6 / 10
alpha = 53.13 °
beta = 36.87 °

Umfang Ballon
U = 20 * pi = 62.832 m
Teilstrecke
U * 36.87 / 360 = 6.435 m
Beide Teilstrecken
6.435 * 2 = 12.87 m