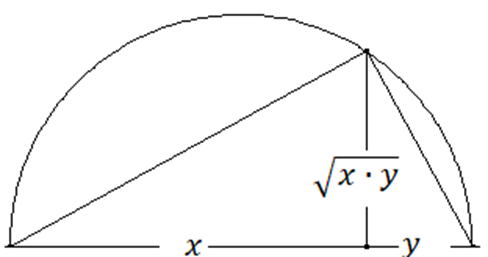
Die Summe zweier positiver reeller Zahlen x und y kann nicht gleich der Wurzel aus ihren Produkt sein. Das kann man algebraisch begründen: x+y=√(x∙y) führt nach Quadrieren und Auflösen nach x zu x1/2= - \( \frac{y}{2} \) ±\( \sqrt{3} \) ·\( \frac{y}{2} \) ·i . Wenn x reell ist, dann ist y komplex und umgekehrt. Geometrisch ergibt sich nach dem Höhensatz von Euklid x+y>√(x∙y).
Die Summe dreier reeller Zahlen a, b und c kann indessen gleich der Wurzel aus ihrem Produkt sein. a+b+c=√(a∙b∙c) führt nach Quadrieren und Auflösen nach a zu
(*) a1/2=\( \frac{1}{2} \)· \( \sqrt{bc(b(c-4)-4c} \) +2(2-c)+2c).
Dies ist eine reelle Lösung insbesondere dann, wenn der Radikand gleich Null ist, also bc(b(c-4)-4c=0 gilt. Dann ist insbesondere b=4c/(c-4). b in (*) eingesetzt, ergibt a=c2/(c-4). Die Summe dreier reeller Zahlen c2/(c-4), 4c/(c-4) und c>4 ist also gleich der Wurzel aus ihrem Produkt. In (bis auf die Reihenfolge) drei Fällen können a, b und c sogar natürliche Zahlen sein:
| 1.Fall | 2.Fall | 3.Fall |
| a | 16 | 18 | 25 |
| b | 8 | 6 | 20 |
| c | 8 | 12 | 5 |
Auch für 4 Summanden kann gelten, dass die Wurzel aus ihren Produkt gleich ihrer Summe ist. Ein Quadrupel derartiger natürlicher Zahlen ist zum Beispiel [15, 10, 2, 3]. Das Prinzip der Herleitung dieses Quadrupels kann aus der Herleitung der zuvor genannten Tripel übernommen werden.
Und schließlich gibt es auch Beispiele für 5 natürliche Zahlen, deren Summe jeweils gleich der Wurzel aus ihrem Produkt ist:
1+2+4+7+14=√(1∙2∙4∙7∙14) und 8+1+1+10+20=√(8∙1∙1∙10∙20).