Hallo,
erst einmal bildest du die 1. Ableitung der Funktion mit der Potenzregel.
\( \begin{array}{l}f(x)=x^{n} \\ f^{\prime}(x)=n \cdot x^{n-1}\end{array} \)
\(f(x)=x^2+3\\ f'(x)=2x \)
Die Ableitung an der Stelle x = 3 ist f'(3). Du setzt also 3 für x in die 1. Ableitung ein.
\(f'(3)=2\cdot 3=6\)
Genauso machst du es für x = -3
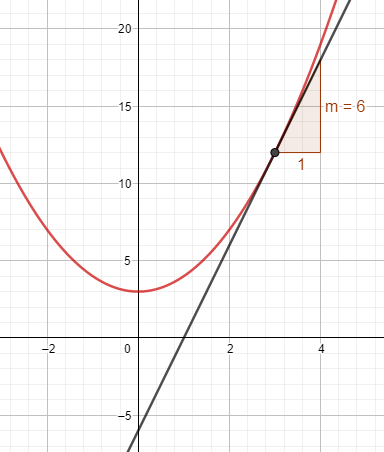
Die Ableitung an einer Stelle entspricht übrigens der Steigung der entsprechenden Tangente.
Gruß, Silvia