Bei der Erklärung steigt ein nicht Mathematiker definitiv aus, hatte eine Teil verstanden und nicht dazu gesagt, dass ich es mit GeoGebra lösen muss.
Ich habe zumindest das mal zur Eingabe in GeoGebra verstanden
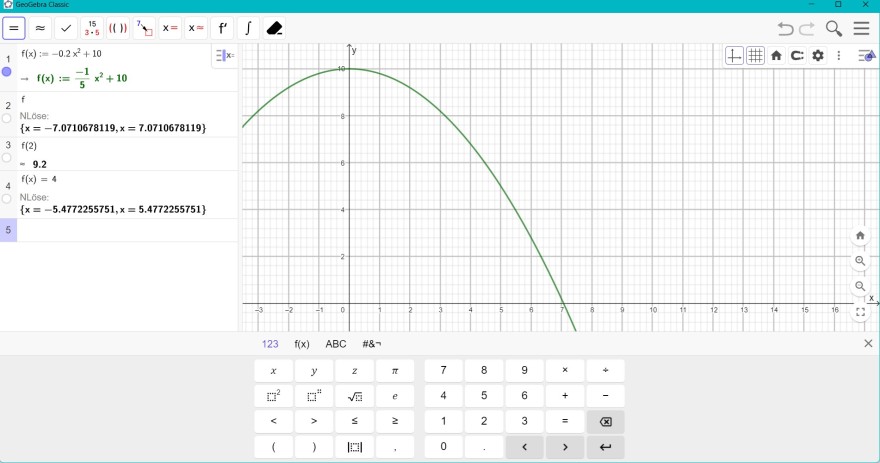
ich gebe die Gleichung in GeoGebra mit f(x):= -0,2x²+10 und löse dann mit f(2) zu 9,2 auf. Dann gebe ich f(x)=4 ein und komme auf x=5,477225751
Die Gleichung sollte ich dann nur mit Hilfe von GeoGebra erstellen, hast Du da eine Idee dazu?
Text erkannt:
\( \left.=\smile \checkmark{ }_{3 \cdot 5}^{15}(1)\right)^{7} \succeq x=x=f^{\prime} \int \)
\begin{tabular}{c|c|c|c|c|c|c|c|c|}
\( x \) & \( y \) & \( z \) & \( \pi \) & 7 & 8 & 9 & \( \times \) & + \\
\hline \( \mathrm{H}^{2} \) & \( \mathrm{D}^{\prime \prime} \) & \( \sqrt{25} \) & \( e \) & 4 & 5 & 6 & + & - \\
\hline\( < \) & \( > \) & \( \leq \) & \( \geq \) & 1 & 2 & 3 & \( = \) & \( \bigotimes \) \\
\hline( & ) & \( 1 \boxminus \) &, & 0 & & \( < \) & \( > \) & \( \leftarrow \)
\end{tabular}
Bei der Zaungleichung, kann sein dass du für dich logische Schritte ausgelassen hast nach
y= m*x+b
und zwischen, die ich nicht sicher bin ob wären: y=9,2, m ist die gesuchte Variable, x ist 4 aber was ist b, denn wie kommst auf folgendes?
m= (4-9,2)/(√30-2) = -1,4954
9,2= -1,4954*2+b
b= 12,19
y= -1,4954x+12,19
Ich muss das mit GeoGebra lösen wo ich sicher was markieren muss und mit x Welle dann löse und der Lehrer will immer ein Bild davon.