Aufgabe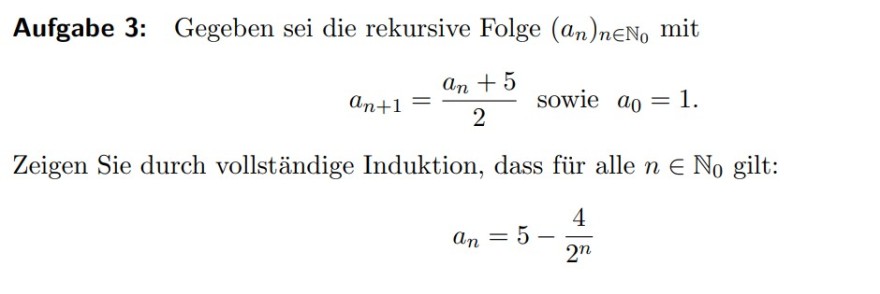
Text erkannt:
Aufgabe 3: Gegeben sei die rekursive Folge \( \left(a_{n}\right)_{n \in \mathbb{N}_{0}} \) mit
\( a_{n+1}=\frac{a_{n}+5}{2} \text { sowie } a_{0}=1 . \)
Zeigen Sie durch vollständige Induktion, dass für alle \( n \in \mathbb{N}_{0} \) gilt:
\( a_{n}=5-\frac{4}{2^{n}} \)
Problem/Ansatz:
irgendwie komme ich leider nicht weiter.
I.A:
n=
a0= 1= 5- 4/2^n
1= 5 - 4/2^0
1= 5-4
1= 1 w.A.
I.V. : Es existiert ein n element von N, sodass an= 5 - 4/2^n gilt.
I.S.:
n -> n+1
an+1= (an+5)/2
(I.V.)=((5-4/2^n)-5)/2
hier komme ich leider nicht weiter.
Über eine Antwort würde ich mehr sehr freuen.
Liebe Grüße
Text erkannt:
\( a_{n}=5-\frac{4}{2^{n}} \)