Berechnen Sie den Fluss von vec{F} =z^{2}\vec{e_{z}}durch die Oberfläche des Körpers

Question

Aufgabe:

Berechnen Sie den Fluss von \(\vec{F} =z^{2}\vec{e_{z}}\) durch die Oberfläche des Körpers
\(K\): \(0≤y≤1-x^{2}, 0≤z≤2-x-y\)

Problem/Ansatz:

Mein Lösungsvorschlag:
Das Vektorfeld \(\vec{F}\) ist parallel zur z-Achse, d.h dass die Flüsse durch alle Begrenzungsflächen (graue Flächen in Bild 2), die parallel zum Vektorfeld \(\vec{F}=\begin{pmatrix} 0\\0\\z^{2} \end{pmatrix} \)  verlaufen, gleich 0 sind. Weiterhin ist der Fluss durch die Bodenfläche (xy-Ebene) ebenfalls 0, da hier z=0 ist. Eine Fläche bleibt übrig, aufgespannt durch \(z=2-x-y\) und begrenzt durch \(y=1-x^{2}\), sowie der xz- und der yz-Ebene (gelbe Fläche in Bild 2).

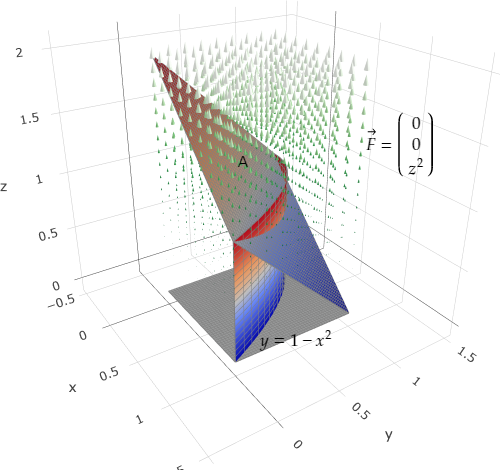
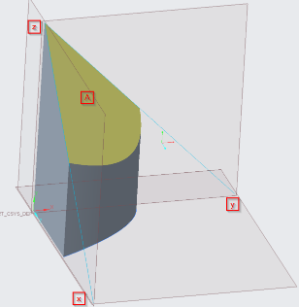
Parametrisierung der Flaeche \(A:\)  \(A(s,t)=\begin{pmatrix} s\\t\\2-s-t \end{pmatrix}, s∈[0,1], t∈[0,1-s^{2}] \)

Fluss \(Φ=\int\int_{A}\vec{F} d\vec{o}=\int\int_{A}\vec{F}·\vec{n} dA\)

\(\vec{n}=A_{s}×A_{t}= \begin{pmatrix} 1\\0\\-1 \end{pmatrix} × \begin{pmatrix} 0\\1\\-1 \end{pmatrix}=\begin{pmatrix}1\\1\\1 \end{pmatrix} \)

"Richtiger" Normalenvektor, da dieser aus dem Koerper herauszeigt.

\(Φ= \int\limits_{0}^{1}\int\limits_{0}^{1-s^{2}} \begin{pmatrix} 0\\0\\(2-s-t)^{2} \end{pmatrix} · \begin{pmatrix} 1\\1\\1 \end{pmatrix} dt ds=\int\limits_{0}^{1}[\frac{1}{3}(s+t-2)^{3}]_{0}^{1-s^{2}} ds =\int\limits_{0}^{1}\frac{7}{3}-3s+2s^{3}-2s^{4}+s^{5}-\frac{1}{3}s^{6} ds= ....=\frac{221}{210}≈1.0524\)

Leider stimmt das Ergebnis nicht und ich kann auch nicht auf die richtige Loesung zugreifen. Wo ist hier mein (Denk)-Fehler? Ich schliesse Rechenfehler aus, da ich das Integral auf Wolfram-Alpha nachgerechnet habe und es kommt das gleiche Ergebnis raus.

Danke schon mal vorab fuer Eure Unterstuetzung!

Answer 1

Aloha :)

Zur Berechnung des Flusses \(\phi\) des Feldes \(\vec F=(0;0;z^2)^T\) durch die Oberfläche des Körpers$$K=\{(x;y;z)\in\mathbb R^3\big|0\le y\le1-x^2\;\land\;0\le z\le 2-x-y\}$$beschreiben wir das Volumen von \(K\) mittels des Ortsvektors$$\vec r=\begin{pmatrix}x\\y\\z\end{pmatrix}\quad;\quad x\in[\pink{-1};1]\;;\;y\in[0;1-x^2]\;;\;z\in[0;2-x-y]$$

Bemerkung: In deinem Lösungsvorschlag ist \(x\in[0;1]\), obwohl z.B. \((-1;0;3)\in K\) gilt.

Den Fluss \(\phi\) findest du mit Hilfe des Gaußschen Satzes \((d\vec f=dV\,\vec\nabla)\):$$\phi=\oiint\limits_{\partial K}\vec F\,d\vec f=\oiint\limits_{\partial K}d\vec f\,\vec F=\iiint\limits_VdV\,\vec\nabla\,\vec F=\int\limits_{x=-1}^1\int\limits_{y=0}^{1-x^2}\int\limits_{z=0}^{2-x-y}\left(\partial_xF_x+\partial_yF_y+\partial_zF_z\right)\,dV$$$$\phantom\phi=\int\limits_{x=-1}^1\int\limits_{y=0}^{1-x^2}\int\limits_{z=0}^{2-x-y}2z\,dz\,dy\,dx=\int\limits_{x=-1}^1\int\limits_{y=0}^{1-x^2}\left[z^2\right]_{z=0}^{2-x-y}\,dy\,dx=\int\limits_{x=-1}^1\int\limits_{y=0}^{1-x^2}(2-x-y)^2\,dy\,dx$$$$\phantom\phi=\int\limits_{x=-1}^1\left[\frac13\left(x+y-2\right)^3\right]_{y=0}^{1-x^2}dx=\frac13\int\limits_{x=-1}^1\left((x-x^2-1)^3-(x-2)^3\right)dx$$$$\phantom\phi=\frac13\int\limits_{-1}^1\left(-x^6+3x^5-6x^4+6x^3-9x+7\right)dx$$Wegen der Symmetrie des Integrationsintervalls liefern alle \(x^n\) mit ungeraden Exponenten \(n\) keinen Beitrag zum Integral:$$\phantom\phi=\frac13\int\limits_{-1}^1\left(-x^6-6x^4+7\right)dx=\frac23\int\limits_0^1\left(-x^6-6x^4+7\right)dx=\frac23\left[-\frac{x^7}{7}-\frac65x^5+7x\right]_0^1$$$$\phantom\phi=\frac23\left(7-\frac17-\frac65\right)=\frac23\cdot\frac{245-5-42}{35}=\frac23\cdot\frac{198}{35}=\frac{132}{35}\approx3,7714$$

Comments

Hallo Tschakabumba,

ich hab tatsaechlich die negative x-Seite des Koerpers unterschlagen.

Vielen Dank fuer Deine Loesung. Das Ergebnis stimmt.