Ich ergänze mal diese Antwort hier, da deine Metrik eine 1 als Index hat.
Eine gängige Verwendung des Index in \( \mathbb R^2\) ist zum Beispiel diese:
\(d_p(u,v) = ||u-v||_p\) für \(u,v \in \mathbb R^2\) und \(p\geq 1\) mit
$$||(x,y)||_p = \sqrt[p]{|x|^p+|y|^p}$$
In deinem Fall hätten wir dann für deine Menge
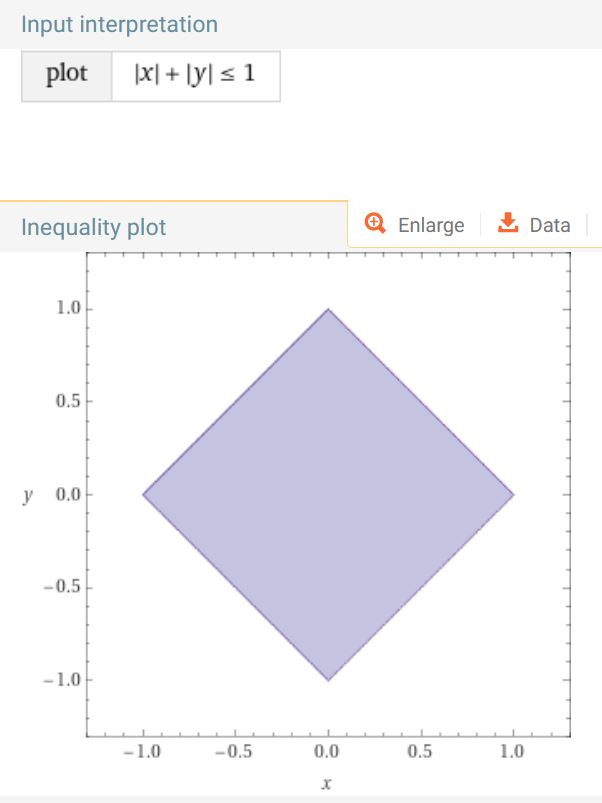
\(\{(x,y) \in \mathbb R^2\;:\; ||(x,y)||_1\leq 1)\} = \{(x,y) \in \mathbb R^2\;:\; |x|+|y|\leq 1)\}\)
Das ist die Einheits"kugel" bzgl. der \(||\cdot ||_1\)-Norm: