Was kennzeichnet die grau hinterlegte Fläche?

Question

Aufgabe:

Es wird ein Gaußtest auf den Erwartungswert durchgeführt. In diesem Fall ist die Verteilung der Teststatistik sowohl unter der Nullhypothese H0 als auch unter der Alternativhypothese H1 bekannt. In der folgenden Grafik sind die entsprechenden Verteilungen zu folgendem Hypothesenpaar abgebildet:

H0: µ0= 11,47      H1: µ1= 14,15

Z1-α ist das entsprechende Quantil zum Signifikanzniveau α und z‾ ist der Wert der Teststatistik unter H0 berechnet mit Hilfe der Stichprobe.

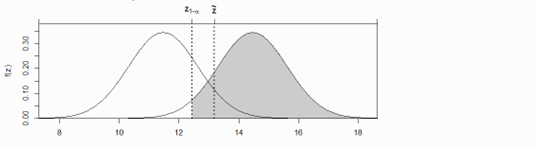
Frage: Was kennzeichhnet die grauhinterlegte Fläche?

a. Die Wahruchenlichkek, de Nullypothese \( H_{4} \) zu verwerfen, wenn diese fahth ise
b. Die wahrscheinlicheit, de Nullhyothese Bo ridht zu venwerfen, wem sie wahr ist.
c. Die Wahrscheinlichieit, die Nullhypothese Bo nicht zu verwerfen, obwohl sie falsch ist.
d. De wahrscheinlichait, die Nulthypothese Ho zuverwerfen, obwohl se wahr ist.
e. Die Wahrocheinlichkeit, unter der Nulhypothese \( H_{1} \) de beobachtete Teststatstik. 1 oder einen in Fichtung der aternativhypothese \( H_{1} \) entremeren Wert zu erhoken.

Antwort: Die Wahrscheinlichkeit, die Nullhypothese H0 zu verwerfen, wenn diese falsch ist.

Problem/Ansatz:

WIe kann ich diesen Test ablesen?

Comments

Morgen früh, bin ich für dich da:D

Answer 1

Die Wahrscheinlichkeit, die Nullhypothese H0 zu verwerfen, wenn diese falsch ist.

Zunächst solltest du erkennen das der Erwartungswert von H1 größer als der von H0 ist. D.h. die rechte Glockenkurve gehört zu H1. Dann ist die Graue Fläche unter dem Graphen von H1. Das kann nur bedeuten das H1 wahr und H0 falsch ist. Da offensichtlich der rechte Teil der Glockenkurve gefärbt ist hat man sich auch für H1 entschieden und nicht für H0. Also ist es die Wahrscheinlichkeit sich für H1 zu entscheiden bzw. H0 zu verwerfen wenn H1 wahr bzw. H0 falsch ist.