Hey,
ich möchte gerne die untere DGL lösen. Seht ihr vielleicht, wie man auf die letzte und vorletzte Zeile kommt? Ich verstehe leider nicht so ganz, wieso man bei der vorletzten Zeile auf beiden Seiten dy hinzufügen darf. Müsste es nicht auf der einen Seite ein dy und auf der anderen Seite ein du sein?
Am meisten Probleme habe ich aber mit der allerletzten Zeile, da ich nicht sehe, inwiefern hier der log angewendet wurde. Seht ihr das vielleicht und könntet mir vielleicht helfen?
LG
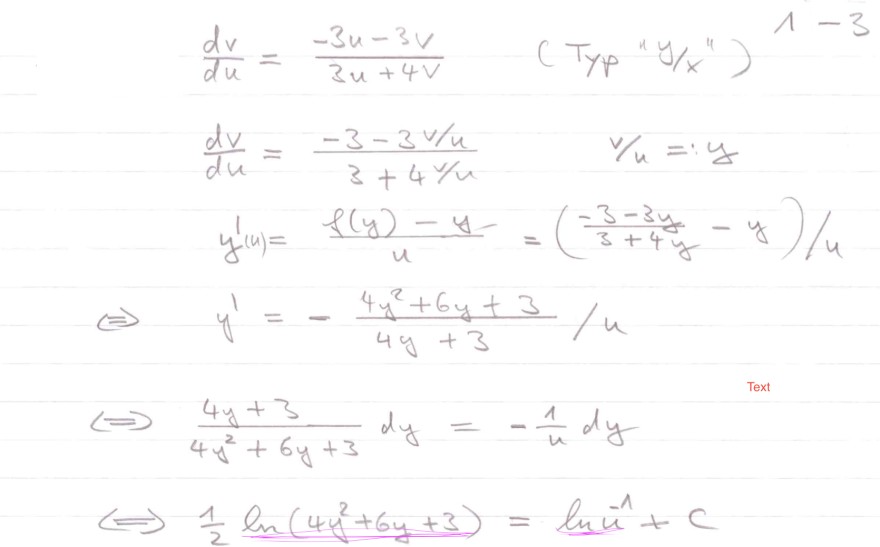
Text erkannt:
\( \begin{array}{ll} & \frac{d v}{d u}=\frac{-3 u-3 v}{3 u+4 v} \quad\left(T_{y p} \| y / x^{\prime \prime}\right)^{1-3} \\ & \frac{d v}{d u}=\frac{-3-3 v / u}{3+4 \% u} \quad \quad v / u=: y \\ & y^{\prime}(u)=\frac{1(y)-y}{u}=\left(\frac{-3-3 y}{3+4 y}-y\right) / u \\ \Leftrightarrow \quad & y^{\prime}=-\frac{4 y^{2}+6 y+3}{4 y+3} / u \\ \Leftrightarrow & \frac{4 y+3}{4 y^{2}+6 y+3} d y=-\frac{1}{u} d y \\ \Leftrightarrow & \frac{1}{2} \ln \left(4 y^{2}+6 y+3\right)=\ln u^{-1}+C\end{array} \)