Konvergiert das gleichmäßig?

Question

Aufgabe:

Es sei \( R>0 \). Untersuchen Sie die durch

\(\displaystyle g_{n}: \overline{B_{R}(0)} \rightarrow \mathbb{R}, \quad x \mapsto\left(1+\frac{x}{n}\right)^{n} \mathrm{e}^{-x}, \quad n \in \mathbb{N}, \)

Problem/Ansatz:

Konvergiert das gleichmäßig?

Comments

Hast Du denn schon geklärt  ob und wie die Funktionenfolge punktweise konvergiert?

---

Ja das tut sie für alle x, nämlich gegen 1

Answer 1

Ich gebe hier eine Argumentation, die auf dem Satz von Dini beruht.

Die Menge \(\overline{B_R(0)}\) ist kompakt.

Weiterhin kann man zeigen, dass auf \(\overline{B_R(0)}\) die Funktionenfolge \(\left(1+\frac xn\right)^n\) ab einem bestimmten Index \(N_0\) für \(n\geq N_0\) monoton wachsend ist.

Damit ist auch die Funktionenfolge \(g_n\) für \(n\geq N_0\) monoton wachsend.

Die Grenzfunktion \(g(x) = 1\) ist stetig.

Damit kann der Satz von Dini angewendet werden und es folgt die gleichmäßige Konvergenz.

Comments

Vielen Dank!

Answer 2

Vielleicht noch eine weniger elegante Lösung: Zu zeigen ist:

$$a_n:=\sup \{|g_n(x)-1)| \mid x \in [-R,R]\} \to 0$$

Es ist

$$g_n'(x)=\exp(-x)\left(1+\frac{x}{n}\right)^{n-1}\left[n\frac{1}{n}-(1+\frac{x}{n})\right]=-\exp(-x)\left(1+\frac{x}{n}\right)^{n-1}\frac{x}{n}$$

Wenn (z.B.) \(n>2R\), dann ist der Graph von \(g_n\) wachsend für negative \(x \in [-R,0)\) und fallend für positive \(x \in (0,R]\)mit \(g_n(0)=1\). Daher ist

$$a_n=\max\{1-g_n(-R),1-g_n(R)\} \to 0$$

Comments

Genügt es nicht zu sagen

(1+x/n)^n geht gegen e^x

e^x*e^-x = e^0 = 1  ???

---

Das wäre nur die punktweise Konvergenz.

---

Danke.

Was bedeutet dann "gleichmäßig"?

---

Einen Link zur Definition wirst du sicher selbst finden, lass mich deshalb eine anschauliche Erklärung anhand des vorliegenden Beispiels versuchen.

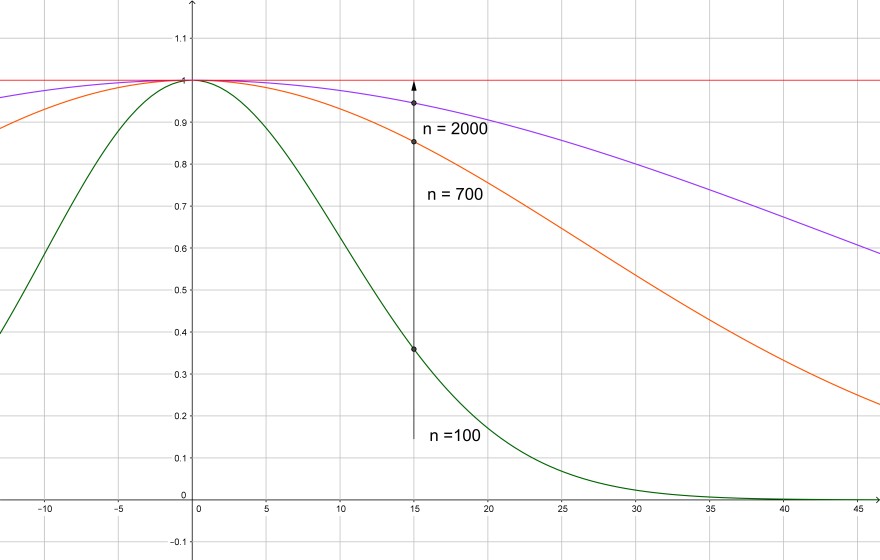
Ich habe die Graphen der Funktionen g_n für drei n-Werte skizziert.

Man erkennt, dass für jeden x-Wert (hier beispielsweise für x=15 gezeichnet) die zugehörigen y-Werte gegen 1 konvergieren (punktweise Konvergenz).
Allerdings dauert es um so länger je größer die x-Werte werden, bis sich die y-Werte dem Grenzwert 1 auf eine bestimmte Distanz genähert haben.
Damit diese Distanz (ε) kleiner als 0,1 wird, die y-Werte also die 0,9-Marke überschreiten, ist für x=4 nur n=100 erforderlich, für x=12 benötigt man schon n=700 und für x=20 sagenhafte n=2000. Tatsächlich wird man für diese Funktionenfolge kein universelles n finden, so dass unabhängig von x alle y-Werte um weniger als ε vom Grenzwert abweichen. Die Funktionenfolge konvergiert daher auf ℝ nicht gleichmäßig gegen g mit g(x)=1. Nun ist aber laut Aufgabenstellung die Definitionsmenge beschränkt, es gibt also maximale |x|-Werte (nur für den angegebenen Beweis unter Benutzung des Dini-Satzes ist die Kompaktheit des Definitionsbereiches, also der Abschluss von B relevant) deshalb können die nicht beliebig groß werden und deshalb gibt es dann irgendwann ein N, so dass für alle x-Werte aus dem Definitionsbereich die y-Werte immer näher als ε an 1 liegen, falls nur der Folgenindex n größer als N ist. Diese letztgenannte Eigenschaft der Funktionenfolge bezeichnet man als gleichmäßige Konvergenz.

---

lass mich deshalb eine anschauliche Erklärung

Das höre ich immer gern. Dankeschön.

Sie können, wenn sie wollen, was ich nie bezweifelt, aber oft vermisst habe

in Sachen unheraklitischer Deutlichkeit.

---

Vielen Dank!