Aufgrund der Preis-Absatz-Funktion für ein Gut ergibt sich, dass 1000 Stück dieses Gutes zu einem Preis von 15 € pro Stück abgesetzt werden können. Durch die Senkung des Preises um 1 € nimmt die Absatzmenge um jewils 1000 Stück zu. Die Durchschnittskosten betragen konstant 10 €.
a) Bestimmen Sie die Funktionsterme der Erlös-, Kosten- und der Gewinnfunktion.
p(x) = a * (x - px) + py = -1/1000 * (x - 1000) + 15 = 16 - x/1000
E(x) = x * p(x) = 16x - x^2/1000
K(x) = 10x
G(x) = E(x) - K(x) = 16x - x^2/1000 - 10x = 6x - x^2/1000
b) Bestimmen Sie die Absatzmenge und den Preis, bei denen der Gewinn am größten ist.
G'(x) = 6 - x/500 = 0
x = 3000 Stück
p(3000) = 19 Euro
c) Geben Sie den maximalen Gewinn an.
G(3000) = 9000 Euro
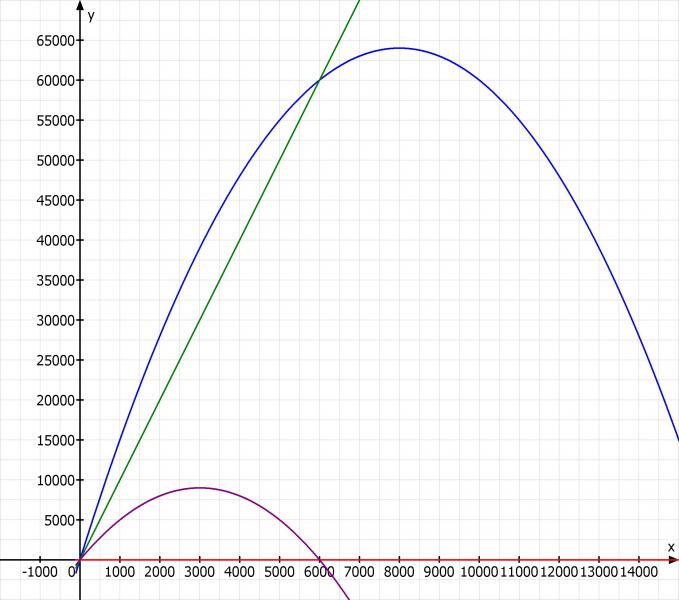
Hier noch eine Skizze