Vielleicht weiß einer von euch beiden (Werner oder hj2166) Rat.
Na ja - etwas habe ich schon heraus bekommen. Auf einen der Kreise kann man getrost verzichten. Wenn man nur \(K_O\) vorgibt, kann man den Punkt \(A\) völlig frei wählen. Der Punkt \(B\) muss dann auf einer Ellipse liegen (rot s.u.). \(D\) muss nicht auf \(K_O\) liegen, aber auf der Geraden durch \(PA\). Die weiteren Punkte \(C\) und \(N\) folgen dann daraus.
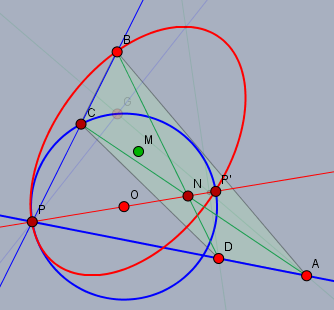
Von der roten Ellipse weiß ich z.Zt. nur, dass sie durch \(P\) und \(P' = K_O \cap g(PO)\) verläuft, und dass sie in \(P\) mit \(K_O\) eine gemeinsame Tangente hat. Sie ist durch die Punkte \(P\), \(D\) und \(A\) sowie den Kreis \(K_O\) eindeutig festgelegt. Wie genau - weiß ich nicht!
Liegt \(B\) auf der Ellipse, so liegen \(P\), \(O\) und \(N\) auf einer Geraden.