Ich mache das mal für a) vor. Vielleicht kannst du es dann für b) zunächst mal selber Probieren. Bei Problemen meldest du dich einfach.
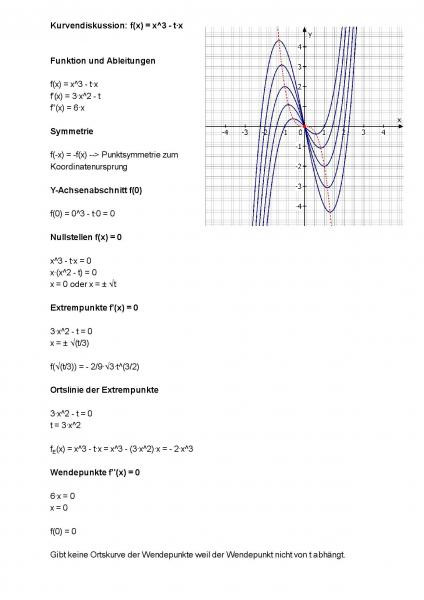
Kurvendiskussion: f(x) = x^3 - t·x
Funktion und Ableitungen
f(x) = x^3 - t·x
f'(x) = 3·x^2 - t
f''(x) = 6·x
Symmetrie
f(-x) = -f(x) --> Punktsymmetrie zum Koordinatenursprung
Y-Achsenabschnitt f(0)
f(0) = 0^3 - t·0 = 0
Nullstellen f(x) = 0
x^3 - t·x = 0
x·(x^2 - t) = 0
x = 0 oder x = ± √t
Extrempunkte f'(x) = 0
3·x^2 - t = 0
x = ± √(t/3)
f(√(t/3)) = - 2/9·√3·t^{3/2}
Ortslinie der Extrempunkte
3·x^2 - t = 0
t = 3·x^2
fE(x) = x^3 - t·x = x^3 - (3·x^2)·x = - 2·x^3
Wendepunkte f''(x) = 0
6·x = 0
x = 0
f(0) = 0
Gibt keine Ortskurve der Wendepunkte weil der Wendepunkt nicht von t abhängt.