Aufgabe:
Bestimmen Sie alle stationäre Punkte von f und geben Sie an, um welchen Typ es sich handelt (Definitionsmenge von f beachten)
Problem/Ansatz:
Mit dem Gradienten habe ich nun versucht, das System zu lösen... Sicher mache ich irgenwo etwas falsch, weil ich auf das Minimum im (1/2; 3/2) kommen sollte. Auf diesen Punkt komme ich gar nicht...
Kann mir bitte jemand zeigen, was ich falsch mache?
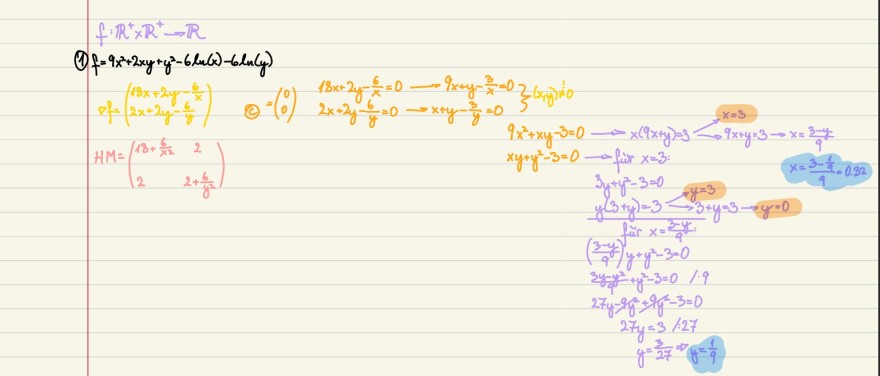
Text erkannt:
\( f: \mathbb{R}^{+} \times \mathbb{R}^{+} \rightarrow \mathbb{R} \)
(1) \( f=9 x^{2}+2 x y+y^{2}-6 \ln (x)-6 \ln (y) \)
\( \begin{array}{l} \nabla f=\left(\begin{array}{l} 18 x+2 y-\frac{6}{x} \\ 2 x+2 y-\frac{6}{y} \end{array}\right) \\ \text { (c) } \left.=\left(\begin{array}{l} 0 \\ 0 \end{array}\right) \quad \begin{array}{l} 18 x+2 y-\frac{6}{x}=0 \longrightarrow 9 x+y-\frac{3}{x}=0 \\ 2 x+2 y-\frac{6}{y}=0 \longrightarrow x+y-\frac{3}{y}=0 \end{array}\right\}(x, y)=0 \\ H M=\left(\begin{array}{cc} 18+\frac{6}{x^{2}} & 2 \\ 2 & 2+\frac{6}{y^{2}} \end{array}\right) \\ x y+y^{2}-3=0 \longrightarrow \text { für } x=3 \\ 3 y+y^{2}-3=0 \quad x y=3 \quad x=\frac{3-\frac{1}{9}}{9}=0.32 \\ \frac{y(3+y)=3 \longrightarrow 3+y-3 \rightarrow y=0}{\operatorname{fir} x=\frac{3-y}{9}} \\ \begin{array}{l} \left(\frac{3-y}{9}\right) y+y^{2}-3=0 \\ 3 y y^{2}+y^{2}-3=0 \quad / \cdot 9 \end{array} \\ 27 y-9 y^{2}+9 y^{2}-3=0 \\ 27 y=3 / 27 \\ y=\frac{3}{27} \Rightarrow y=\frac{1}{9} \\ \end{array} \)