Berechnen Sie den Inhalt der endlichen Fläche, die von f(x) und g(x) begrenzt wird.

Question

Aufgabe:

Gegeben sind die Funktionen f(x) und g(x) mit den Gleichungen

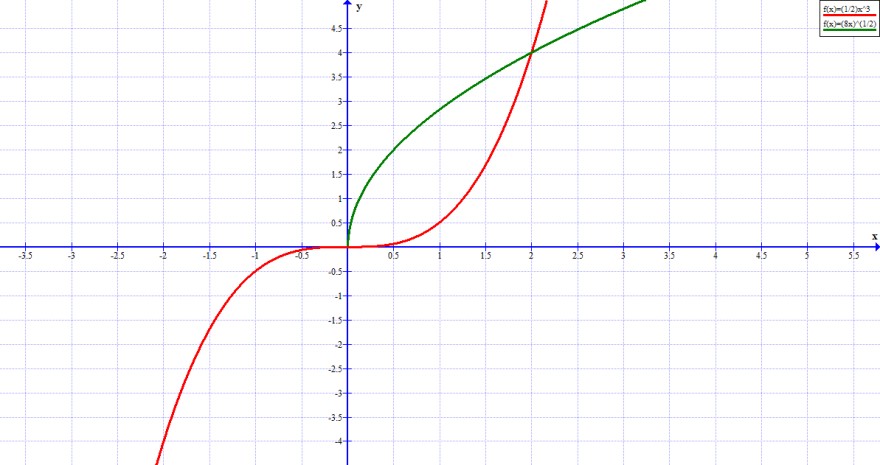
        f(x) = \( \frac{1}{2} \) \( x^{3} \) und  g(x) = \( \sqrt{8x} \)

(a)  Errechnen Sie die Schnittpunkte von f(x) und g(x) und nutzen Sie diese Information, um                         die beiden Funktionsgraphen zu skizzieren.

(b)  Berechnen Sie den Inhalt der endlichen Fläche, die von f(x) und g(x) begrenzt wird.

(c)  Wie gross ist die längste Strecke [AB], die sich diesem Flächenstück einbeschreiben lässt,

    wenn [AB]  parallel zur…
    i. …y-Achse
    ii. …x-Achse
    verlaufen soll?

Problem/Ansatz:

Extremwert - Aufgaben unter (c)

Ich habe (a) und (b) gelöst. Ich habe Problem mit (c)! Bitte um Hilfe zu (c). Vielen Dank

Answer 1

i.) Maximiere: f(x)-g(x), Abstand der y-Koordinaten

ii) Abstand der x-Werte von f und g maximieren.

Dazu würde ich die Umkehrfunktionen verwenden. (Ist nur so eine Idee, weil ich nichts anderes wüsste,

damit eine Differenzfunktion entsteht, die man maximieren kann)

Comments

Das ist ein zielführender und einfacher Weg. Direkt die Formel zur Ableitung der Umkehrfunktion zu benutzen wäre auch möglich.
Kontrollergebnis : y = (128/27)^0,2 und Δx_max ≈ 1,1647

---

Vielen Dank.

Vlt. können Sie noch kurz die Alternative erklären und wie man draufkommt.

Ich weiß auch offen gesagt nicht, warum mein Verlegenheitsansatz trifft.

Die Differenz vom x-Werten zu maximieren sehe ich hier zum ersten Mal.

Sie können das sicher nachvollziehbar erklären, worum ich Sie bitten möchte.

---

Der gesuchte Abstand Δx = b-a ist dort maximal, wo die Tangenten t_f und t_g parallel verlaufen, also wo die Steigung von f an der Stelle b gleich der Steigung von g an der Stelle a ist, wobei f(b)=g(a)=y zu beachten ist.

f'(b)=3/2b^2 , g'(a)=8/(2*√(8a)) und y=b³/2=√(8a) ergibt
3/2b^2 = 4/(b³/2) also b=(16/3)^1/5 daraus folgend y=(128/27)^1/5 und a=1458^-1/5

---

Vielen Dank für die ausführliche, nachvollziehbare und optisch sehr schöne

Antwort. Perfekt. Chapeau!

An Tangenten habe ich gedacht, konnte es aber nicht weiter umsetzen.

In der Prüfung kommt wohl kaum jemand drauf, der das zum ersten Mal

lösen soll. Die 15-Punkte-Bremse ???

---

In der Prüfung kommt wohl kaum jemand drauf

Braucht er ja auch nicht, wenn er den von dir vorgeschlagenen Weg über die Umkehrfunktionen geht.

---

An Tangenten habe ich gedacht

Es ist ja auch letztlich dasselbe, was du hier bei ci) gemacht hast :

um Δy=a-b=g(x)-f(x) ( solltest du verbessern zu  = |f(x)-g(x)| ) zu maximieren, bildest du die Ableitung von Δy und setzt diese gleich 0, aber g'(x)-f'(x)=0 ist doch g'(x)=f'(x) also Gleichheit der Steigungen der Tangenten t_g an der Stelle x und t_f an der Stelle x.