In welchem Verhältnis der Flächeninhalte teilt der Graph von f die Fläche dieses Dreiecks?

Question

Text erkannt:

INTEGAALAECHNUNG
17.
Die Funktion \( f \) ist gogobon durch \( f(x)=\frac{1}{4} x^{4}-\frac{3}{2} x^{2}+\frac{1}{4} \).
a) Untersuche und zeichne den Graphen von \( f \).
b) Berechno den Filicheninhalt der von dor Vorbindungsgoriden der Tiefpunkte und dem Graphen von f oingeschlossenon Fliche.
c) Die boiden Wendetangenten und die Verbindungsgerade der Wendepunkto bildon oin Droieck. In welchem Verhältnis der Flilcheninhalte toilt der Graph von \( f \) die Fliche dieses Dreiecks?

Aufgabe:

Text erkannt:

Für \( k>0 \) ist die Funktion \( f_{k} \) gegeben durch \( f_{k}(x)=-\frac{1}{k} x^{5}+k x^{3} \).
33.
a) Untersuche und zeichne den Graphen von \( f_{k} \) für \( k=3 \).
b) Bestimme \( k \) so, dass der Flächeninhalt der Fläche zwischen dem Graphen von \( f_{k} \) und der 1 . Achse \( \frac{16}{3} \) beträgt.

Für \( 0<k<3 \) ist die Funktion \( f_{k} \) gegeben durch \( f_{k}(x)=-x^{2}+k x \). Wähle \( k \), sodass die Fläche zwischen
34. dem Graphen von \( f_{k} \) und der 1 . Achse zwischen den Geraden mit \( x=0 \) und \( x=3 \) minimal wird.
35.

Comments

Es wäre besser, du würdest jede der drei Aufgaben einzeln eingeben. Es wäre auch hilfreich zu wissen, was du schon gerechnet hast bzw. wo genau deine Probleme sind.

---

Lösung zu 17 a

zu b)

zu c)

Answer 1

17c)

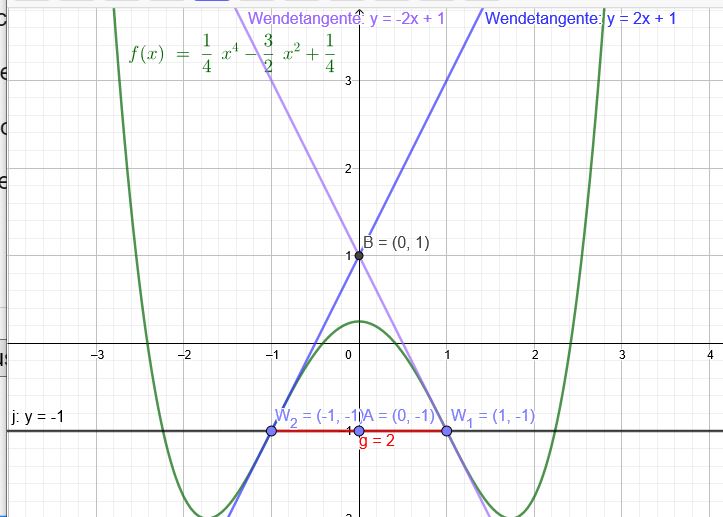
\( f(x)=\frac{1}{4} x^{4}-\frac{3}{2} x^{2}+\frac{1}{4} \)

\( f´(x)= x^{3}-3 x\)

\( f´´(x)= 3x^{2}-3 \)

Wendepunkte:

\(  3x^{2}-3=0 \)

\(  x_1=1 \)     \( f(1)=-1\)

\(  x_2=-1 \)   \( f(-1)=-1\) 

Bestimmung der Wendetangenten:

\( f´(1)= (1)^{3}-3* (1)=-2\)

\(  \frac{y+1}{x-1}=-2\)

Die Tangente schneidet die y-Achse in:

\(  y=1\)

Die Verbindungsgerade zwischen den Wendepunkten hat die Funktion \(y=-1\). Diese schneidet die

y-Achse in \(A(0|-1)\) Somit beträgt die Höhe des Dreiecks \(2LE\).

Die Fläche des Dreiecks ist somit   \(A=2FE\).

Berechne nun die Fläche unter der Parabel und bestimme das Verhältnis der Flächeninhalte.