Wahrscheinlichkeit berechnen kaputter Würfel

Question

Aufgabe:

bei einem Würfel ist,eine Ecke beschädigt. Daher wird angenommen, dass die Wahrscheinlichkeit eine bestimmte Augenzahl zu werfen nicht für alle Augenzahlen gleich groß ist. Es wurden 2 Wurfserien mit jeweils 50 Würfen durchgeführt.

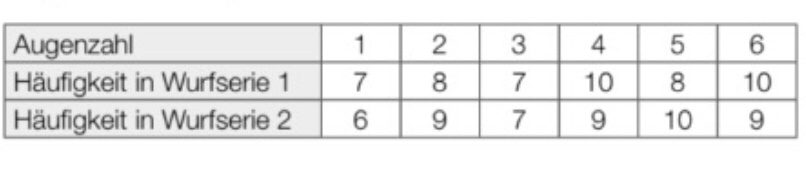
In der folgenden Tabelle werden die absoluten Häufigkeiten zusammengefasst

Problem/Ansatz:

geben sie einen Schätzwert für die Wahrscheinlichkeit p in %an, mit diesem Würfel eine 6 zu werfen

Text erkannt:

\begin{tabular}{|l|c|c|c|c|c|c|}
\hline Augenzahl & 1 & 2 & 3 & 4 & 5 & 6 \\
\hline Häufigkeit in Wurfserie 1 & 7 & 8 & 7 & 10 & 8 & 10 \\
\hline Häufigkeit in Wurfserie 2 & 6 & 9 & 7 & 9 & 10 & 9 \\
\hline
\end{tabular}

Answer 1

geben sie einen Schätzwert für die Wahrscheinlichkeit p in %an, mit diesem Würfel eine 6 zu werfen

In 19 von 100 Würfen wurde eine 6 gewürfelt. Damit ist ein Schätzwert einfach

p = 19/100 = 0.19 = 19%.

Answer 2

Schätzwert für die Wahrscheinlichkeit p in %, mit diesem Würfel eine 6 zu werfen, ist das arithmetische Mittel aus \( \frac{10}{50} \) und \( \frac{9}{50} \).  (\( \frac{10}{50} \) + \( \frac{9}{50} \))/2=19%,