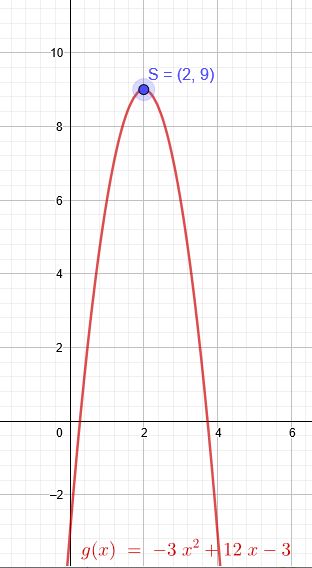
b)
\(g(x) =-3x^2 + 12x-3|+3\)
\(g(x)+3 =-3x^2 + 12x |:(-3)\)
\(\frac{g(x)+3}{-3}=x^2 -4x \)
\(\frac{g(x)+3}{-3} - (\frac{4}{2})^2=(x - \frac{4}{2})^2 \)
\(\frac{g(x)+3}{-3} + 4=(x - 2)^2 |*(-3) \)
\(g(x)+3 - 12=-3*(x - 2)^2 \)
\(g(x)-9=-3*(x - 2)^2 |+9 \)
\(g(x)=-3*(x - 2)^2+9 \)
\(S(2|9)\)