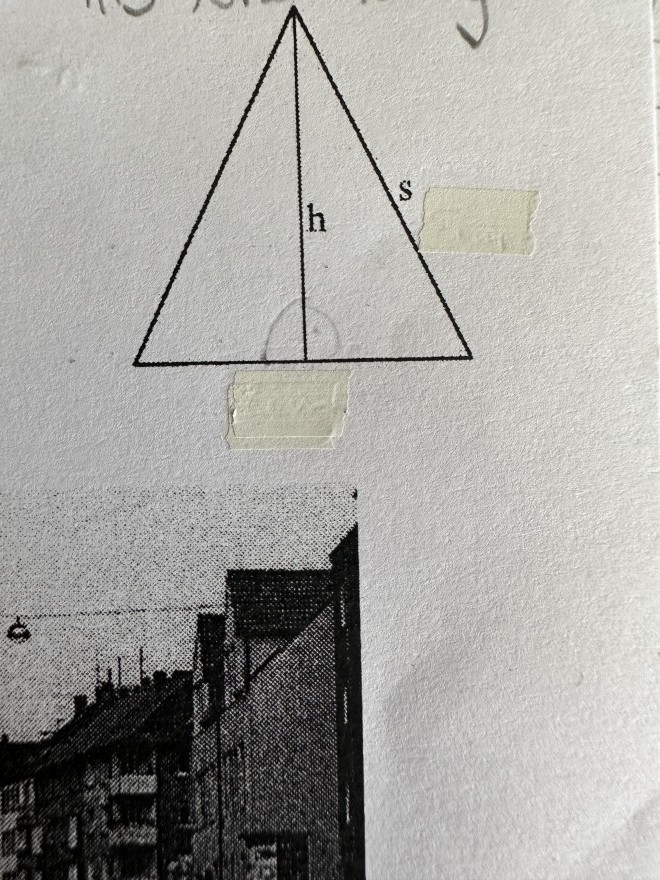
Aufgabe: Von den drei Größen c, s und h eines gleichschenkligen Dreieck sind zwei gegeben . Berechne die dritte.
s = 3,3 km
h = 2.9 km
Problem/Ansatz:
Ich habe die Formel vom Satz des Pythagoras, von den beiden Kathetensätzen und vom Höhensatz .
Ich kann hier aber nicht Satz des Pythagoras anwenden, weil ich keinen rechten Winkel habe . Man könnte das mit der Höhe unterteilen, da hätte ich wieder einen rechten Winkel. Aber ich weiß nicht, ob ich das machen darf. Ich kann diese 4 Formeln alle nicht anwenden.
Wie muss ich vorgehen ?