Hallo,
Ich stehe echt auf dem Schlauch, ...
es wäre hilfreich, wenn Du etwas genauer beschreibst, wo es nicht mehr weiter geht. Dann kann man auch gezielter antworten.
Es gilt zunächst die Schnittpunkte von jeweils zwei Geraden zu berechnen. Z.B. \(g\) und \(h\). Der mögliche Schnittpunkt wird ermittelt, indem man die beiden Geraden gleich setzt und nach \(r\) und \(s\) auflöst:$$\begin{aligned}g(r)&=h(s)\\\begin{pmatrix}0\\ -1\\ 2\end{pmatrix} + r\begin{pmatrix}-2\\ 2\\ 1\end{pmatrix} &= \begin{pmatrix}3\\ -1\\ -2\end{pmatrix} + s\begin{pmatrix}-2\\ -4\\ 6\end{pmatrix}\\ r\begin{pmatrix}-2\\ 2\\ 1\end{pmatrix} - s\begin{pmatrix}-2\\ -4\\ 6\end{pmatrix} &= \begin{pmatrix}3\\ -1\\ -2\end{pmatrix} - \begin{pmatrix}0\\ -1\\ 2\end{pmatrix}=\begin{pmatrix}3\\ 0\\ -4\end{pmatrix}\end{aligned}$$Addition der ersten beiden Zeilen $$\begin{aligned}-2r +2s &= 3\\ 2r + 4s &= 0\end{aligned}$$gibt $$6s = 3 \implies s = \frac{1}{2} $$Dies in die erste Zeile einsetzen gibt$$-2r + 2\cdot \frac{1}{2} = 3 \implies r=-1$$Zur Kontrolle - ob der Schnittpunkt überhaupt existiert - muss diese Ergebnis noch in die dritte Zeile eingesetzt werden:$$\begin{aligned}r - 6s &= -4\\ (-1) - 6\cdot \frac{1}{2} &= -4\space \checkmark\end{aligned}$$Die Gleichung geht auf, also existiert ein Schnittpunkt, die Geraden sind nicht windschief. Einsetzen des Ergebnisses in einer der beiden Geraden liefert seine Koordinaten:$$A = g(-1) = \begin{pmatrix}0\\ -1\\ 2\end{pmatrix} + (-1)\cdot\begin{pmatrix}-2\\ 2\\ 1\end{pmatrix} = \begin{pmatrix}2\\ -3\\ 1\end{pmatrix}$$Die Werte der anderen beiden Schnittpunkte kannst Du der Geoknecht3D-Skizze entnehmen
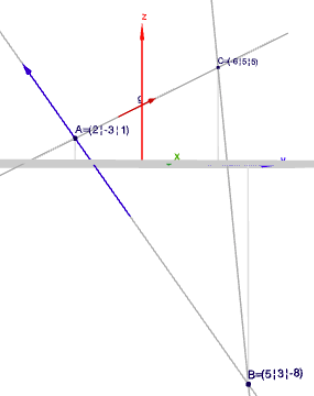
(klick auf das Bild)
Für die Berechnung des Umfangs muss man jeweils den Abstand der Punkt |AB|, |BC| und |CA| berechnen. Berechne dazu jeweils die Differenz zweier Punkte und dann ziehe die Wurzel aus der Quadratesumme der Koordinaten - das hast Du doch bestimmt schon gemacht (frei nach Pythagoras).
Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner