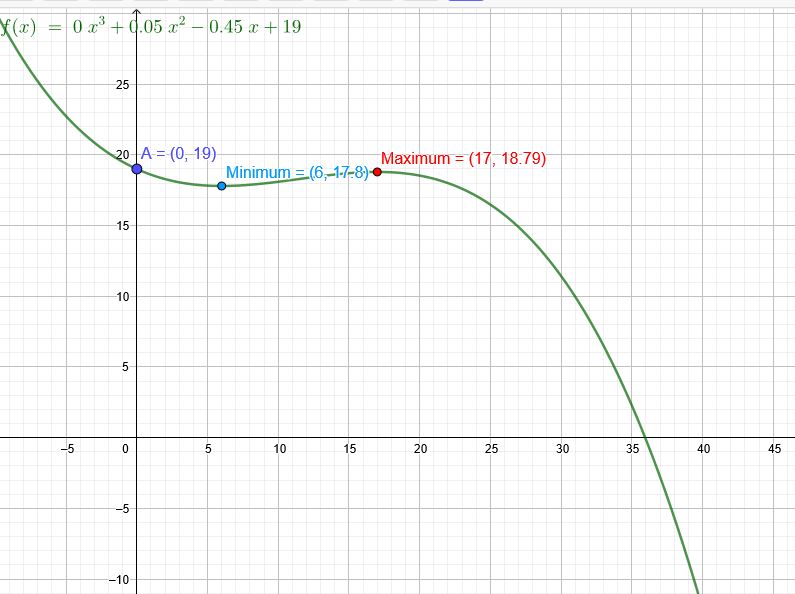
\(f(x)=a*x^3+b*x^2+c*x+d\)
\(A(0|19)\):
\(f(0)=a*0^3+b*0^2+c*0+d\) → 1.) \(d=19\)
\(B(6|17,8)\):
\(f(6)=a*6^3+b*6^2+c*6+19\) → 2.) \(216a+36b+6c+19=17,8\)
Minimum bei \(B(6|...)\)
\(f´(x)=3a*x^2+2b*x+c\)
\(f´(6)=3a*6^2+2b*6+c\) → 3.) \(3a*6^2+2b*6+c=0\)
17Uhr am höchsten:
\(f´(17)=3a*17^2+2b*17+c\) → 4.) \(3a*17^2+2b*17+c=0\)
\(a≈-0,00148148\) \(b≈0,0511111\) \(c≈-0,453333\) \(d=19\)
\(f(x)=-0,00148148*x^3+0,0511111*x^2-0,453333*x+19\)
Wann die Temperatur am stärksten gestiegen ist, findest mit der Berechnung des Wendepunktes.
\(f´´(x)=0\)