Grenzwert berechnen und Konvergenz prüfen

Question

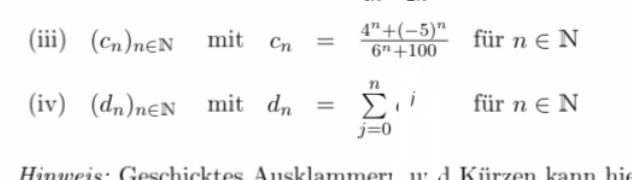
Text erkannt:

(iii) \( \left(c_{n}\right)_{n \in \mathbb{N}} \) mit \( \quad c_{n}=\frac{4^{n}+(-5)^{n}}{6^{n}+100} \) für \( n \in \mathbb{N} \)
(iv) \( \left(d_{n}\right)_{n \in \mathbb{N}} \) mit \( \quad d_{n}=\sum \limits_{j=0}^{n}, i \quad \) für \( n \in \mathbb{N} \)

Aufgabe:

Comments

Du weißt schon, dass man die iv) nicht erkennt :)

---

Für die i) solltest du durch 6^n teilen und begründen, welche Summanden gegen 0 konvergieren

---

Text erkannt:

(iv) \( \left(d_{n}\right)_{n \in \mathrm{N}} \quad \) mit \( \quad d_{n}=\sum \limits_{j=0}^{n} q^{j} \quad \) für \( n \in \mathbb{N} \)

Answer 1

iii) Kürze mit 6^n, das ohnehin gewinnt, weil am schnellsten wachsend.

lim (0+0)/(1+0) = 0