Aufgabe:
Bestimme die Extremapunkte der mehrdimensionalen Funktion
Problem/Ansatz:
Wenn ich das Gleichungssystem nach der ersten Methode löse, bekomme ich die richtige Stationäre Punkte heraus: (0,0) und (-2,-2).
Wenn ich das Gleichungssystem mit der zweiten Methode löse, komme ich auf (0,0) und (-2,2)… Was mache ich falsch? Leider weiss ich monetan nicht weiter.
Leider muss ich mein Screenshor hochladen, da die Funktion zum Konvertieren nur folgendes Herausspukt:
“
(b) \( f=x^{3}+y^{3}+6 x y \)
\( \begin{array}{l} \left(\begin{array}{cc} 6 x & 6 \\ 6 & 6 y \end{array}\right) \\ \end{array} \)
\( x \)
“
Danke und LG!
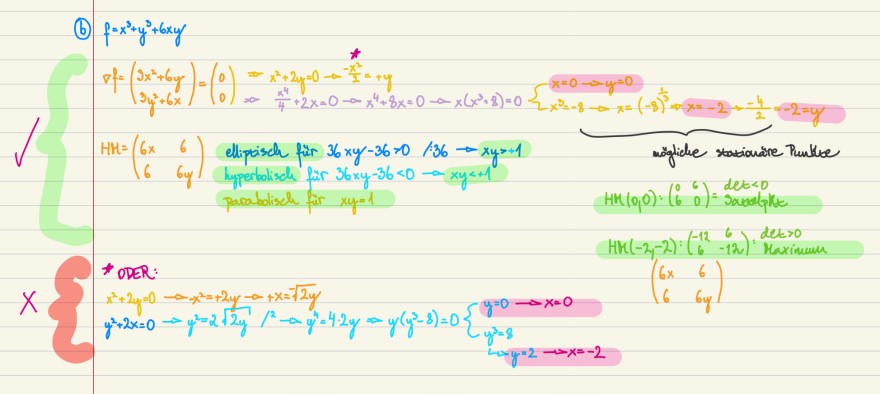
Text erkannt:
(b) \( f=x^{3}+y^{3}+6 x y \)
\( \begin{array}{l} \left(\begin{array}{cc} 6 x & 6 \\ 6 & 6 y \end{array}\right) \\ \end{array} \)
\( x \)