Aufgabe:
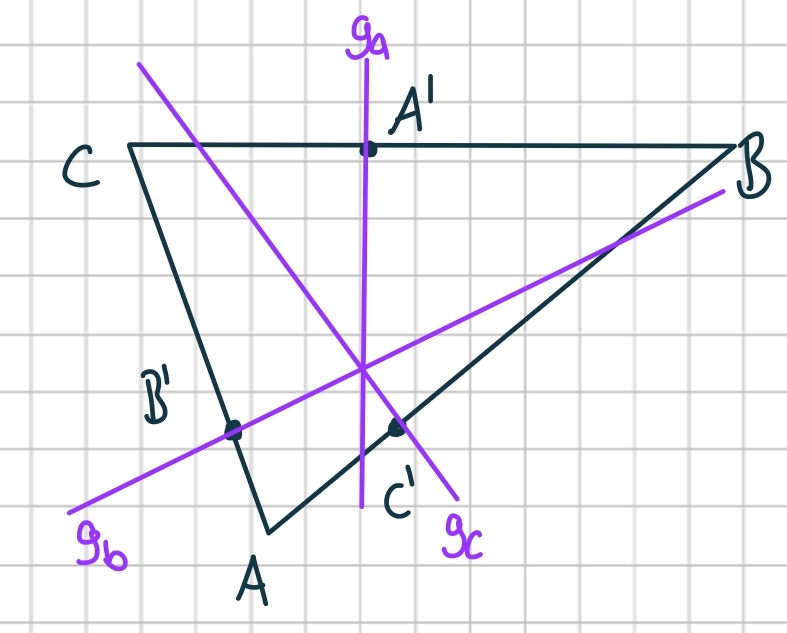
Es seien ABC ein euklidisches Dreieck und A'∈ BC (Strecke) B'∈ CA (Strecke) C'∈ AB (Strecke) Punkte auf den Dreiecksseiten. Weiter seien ga , gb , gc die Orthogonalen zu den jeweiligen Dreiecksseiten durch die Punkte A', B' sowie C'.
Beh: ga , gb , gc schneiden sich in einem Punkt ⇔ |AC'|2 + |BA'|2 + |CB'|2 = |A'C|2 + |B'A|2 + |C'B|2
Problem/Ansatz:
Leider weiß ich nicht wie ich die Hin und Rückrichtung zeigen kann?
Da die Geraden nicht unbedingt die Mittelsenkrechten sind, ist der Schnittpunkt nicht unbedingt der Umkreismittelpunkt.
Bin über jede Hilfe dankbar