Text erkannt:
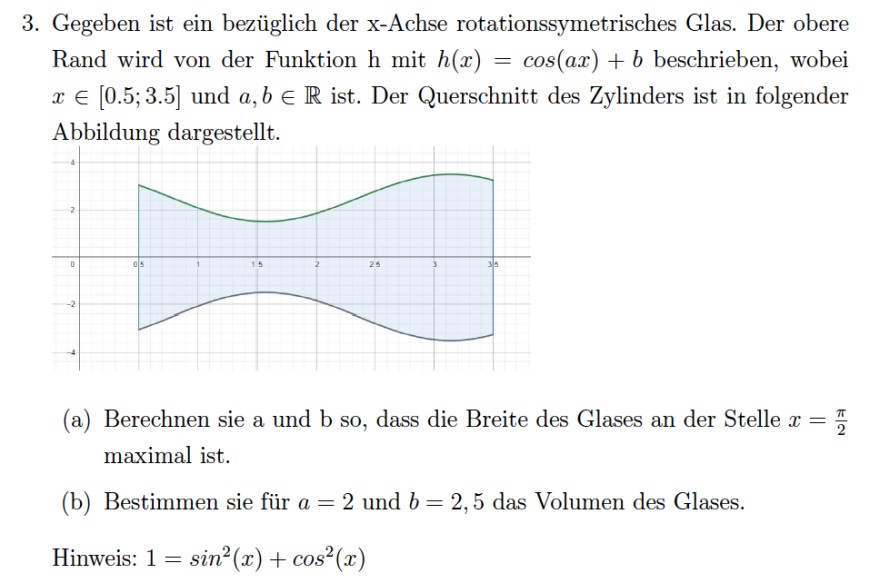
3. Gegeben ist ein bezüglich der \( \mathrm{x} \)-Achse rotationssymetrisches Glas. Der obere Rand wird von der Funktion h mit \( h(x)=\cos (a x)+b \) beschrieben, wobei \( x \in[0.5 ; 3.5] \) und \( a, b \in \mathbb{R} \) ist. Der Querschnitt des Zylinders ist in folgender Abbildung dargestellt.
(a) Berechnen sie a und b so, dass die Breite des Glases an der Stelle \( x=\frac{\pi}{2} \) maximal ist.
(b) Bestimmen sie für \( a=2 \) und \( b=2,5 \) das Volumen des Glases.
Hinweis: \( 1=\sin ^{2}(x)+\cos ^{2}(x) \)
Würde meine Antwort hier so ausreichen? Ich verzweifle
bei a) habe ich folgendes gedacht:
Um die Breite des Glases an der Stelle x = π/2 zu maximieren, müsste ich den Scheitelpunkt der Funktion h(x) finden. Da h(x) = cos(ax) + b eine cosinusförmige Funktion ist, befindet sich der Scheitelpunkt bei x = 0. Um den Faktor a zu berechnen, betrachten wir die Ableitung der Funktion h(x).
h'(x) = -a * sin(ax)
Setzen wir x = 0 ein:
h'(0) = -a * sin(0) = 0
Da der Ableitungswert an der Stelle x = 0 gleich 0 sein muss, wüsste ich dann, dass a * sin(0) = 0. Die Sinusfunktion hat bei x = 0 ein Maximum oder Minimum, also sin(0) = 0. Das bedeutet, dass a beliebig sein kann.
Um b zu berechnen, habe ich x = π/2 in die Funktion h(x) eingesetzt:
h(π/2) = cos(a * π/2) + b
Um die Breite des Glases zu maximieren, muss der Cosinuswert maximal sein, was bei cos(0) = 1 der Fall ist. Daher setzen wir a * π/2 = 0 und lösen nach b auf:
h(π/2) = cos(0) + b
1 = 1 + b
b = 0
Die Werte a = beliebig und b = 0 erfüllen die Bedingung, dass die Breite des Glases an der Stelle x = π/2 maximal ist.
h'(x) = -a * sin(ax)
Setzen wir x = 0 ein:
h'(0) = -a * sin(0) = 0
Da der Ableitungswert an der Stelle x = 0 gleich 0 sein muss, wissen wir, dass a * sin(0) = 0. Die Sinusfunktion hat bei x = 0 ein Maximum oder Minimum, also sin(0) = 0. Das bedeutet, dass a beliebig sein kann.
Um b zu berechnen, setzen wir x = π/2 in die Funktion h(x) ein:
h(π/2) = cos(a * π/2) + b
Um die Breite des Glases zu maximieren, muss der Cosinuswert maximal sein, was bei cos(0) = 1 der Fall ist. Daher setzen wir a * π/2 = 0 und lösen nach b auf:
h(π/2) = cos(0) + b
1 = 1 + b
b = 0
Die Werte a = beliebig und b = 0 erfüllen die Bedingung, dass die Breite des Glases an der Stelle x = π/2 maximal ist.
bei b) habe ich folgendes:
Um das Volumen des Glases zu berechnen, müssen wir den Querschnitt des Zylinders integrieren. Der Querschnitt wird durch die Funktion h(x) = cos(ax) + b beschrieben.
Für a = 2 und b = 2,5 haben wir:
h(x) = cos(2x) + 2,5
Die maximale Höhe des Glases h_max ergibt sich, wenn h(x) = 0, also:
0 = cos(2x) + 2,5
--> cos(2x) = -2,5 und nach x auflösen
Angenommen, wir erhalten die Lösungen x_1 ≈ 0,573 und x_2 ≈ 2,568.
Das Volumen des Glases ergibt sich dann zu:
V = ∫(von 0,573 bis 2,568) [π * (cos(2x) + 2,5)^2] dx
Text erkannt:
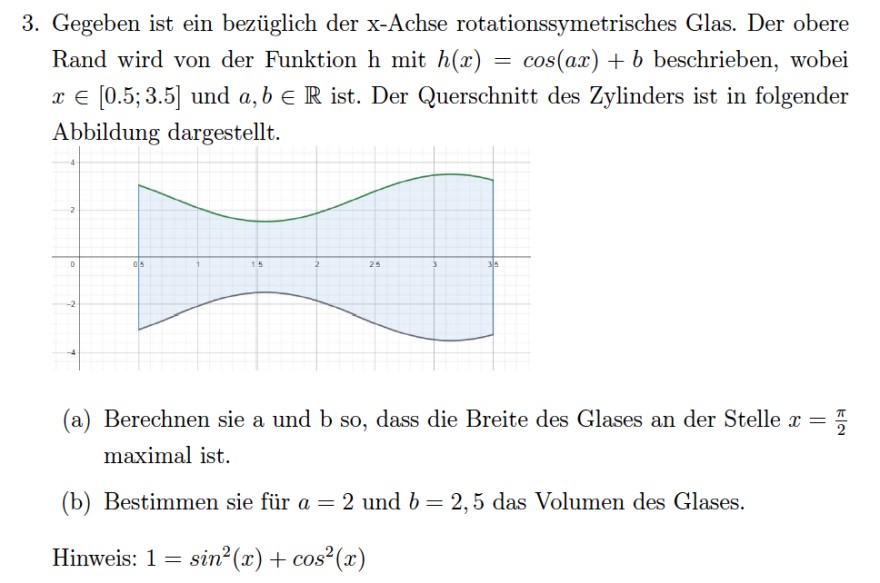
3. Gegeben ist ein bezüglich der \( \mathrm{x} \)-Achse rotationssymetrisches Glas. Der obere Rand wird von der Funktion h mit \( h(x)=\cos (a x)+b \) beschrieben, wobei \( x \in[0.5 ; 3.5] \) und \( a, b \in \mathbb{R} \) ist. Der Querschnitt des Zylinders ist in folgender Abbildung dargestellt.
(a) Berechnen sie a und b so, dass die Breite des Glases an der Stelle \( x=\frac{\pi}{2} \) maximal ist.
(b) Bestimmen sie für \( a=2 \) und \( b=2,5 \) das Volumen des Glases.
Hinweis: \( 1=\sin ^{2}(x)+\cos ^{2}(x) \)
