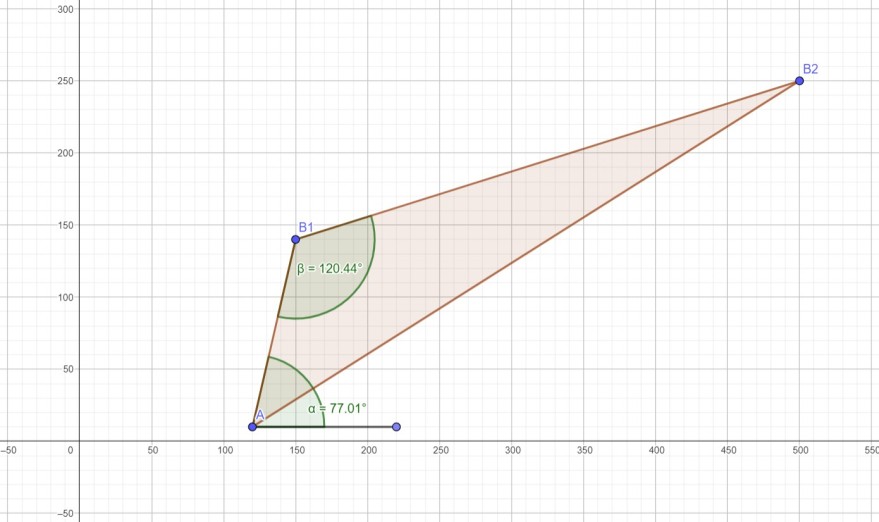
Bei einem Ruderbewerb müssen auf einem See zwei Bojen an den Positionen B1(150 | 140) und B2(500 | 250) passiert werden. Danach soll zum Startpunkt zurückgekehrt werden. Ein Ruderteam startet im Punkt A(120 | 10) (Angaben in Meter).
a) Berechne, in welchem Winkel zur Horizontalen das Team die erste Boje B1 mindestens ansteuern sollte.
AB1 = [30, 130]
arctan(130/30) = 77.01°
b) Ermittle den Winkel zwischen B1A und B1B2.
B1A = [-30, -130]
B1B2 = [350, 110]
ARCCOS([-30, -130]·[350, 110]/(ABS([-30, -130])·ABS([350, 110]))) = 120.44°
c) Berechne, welche Wasserfläche durch den Parcours A, B1, B2 eingeschlossen wird.
1/2·ABS([-30, -130] ⨯ [350, 110]) = 21100 m²
Skizze