Aufgabe: Wir sollen die offene Mengen mit Definition beweisen
Problem/Ansatz: Naja die Richtung => wäre ja: Sei M offen, so ist IR \ M abgeschlossen, d.h in jeder konvergente Folge von Komplement in IR\M isr auch der Grenzwert in IR \ M
Aber wie kommt kommen dann die Rückschlüsse zur Definition? 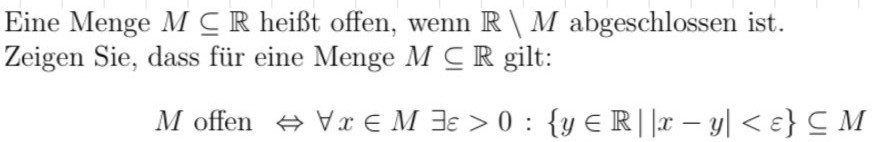
Text erkannt:
Eine Menge \( M \subseteq \mathbb{R} \) heißt offen, wenn \( \mathbb{R} \backslash M \) abgeschlossen ist. Zeigen Sie, dass für eine Menge \( M \subseteq \mathbb{R} \) gilt:
\( M \text { offen } \Leftrightarrow \forall x \in M \exists \varepsilon>0:\{y \in \mathbb{R}|| x-y \mid<\varepsilon\} \subseteq M \)