Aufgabe:
Gegeben ist die Funktion f mit der Gleichung: f(x)=x4 −8 x⋅3 +6 x⋅2 +40 x⋅, x ∈IR.
Die Steigung einer Sekante s durch den Punkt P (4 | 0) und einen weiteren Punkt P2 des Graphen von f soll sich um weniger als 0,1 von der Steigung der Tangente t unterscheiden.
Lösung:
Text erkannt:
\begin{tabular}{|l|l|l|}
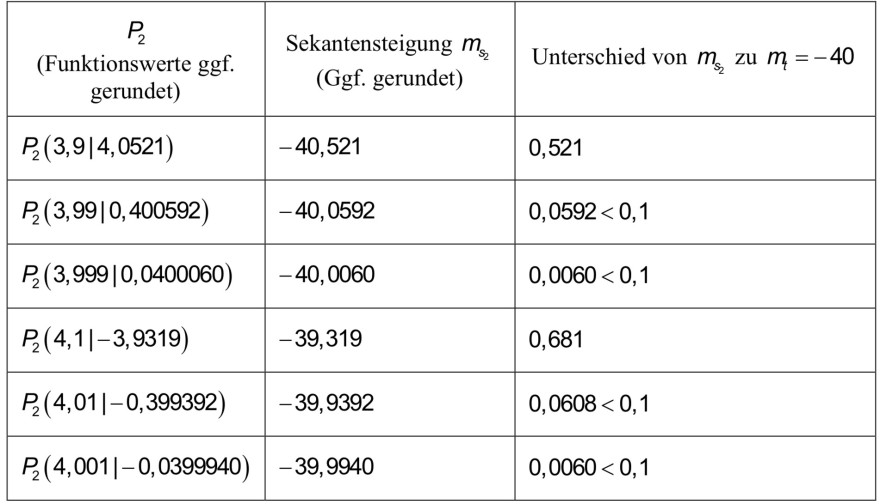
\hline \( \begin{array}{c}P_{2} \\ \text { (Funktionswerte ggf. } \\ \text { gerundet) }\end{array} \) & \multicolumn{1}{|c|}{\( \begin{array}{c}\text { Sekantensteigung } m_{s_{2}} \\ \text { (Ggf. gerundet) }\end{array} \)} & \multicolumn{1}{|c|}{ Unterschied von \( m_{s_{2}} \) zu \( m_{\imath}=-40 \)} \\
\hline\( P_{2}(3,9 \mid 4,0521) \) & \( -40,521 \) & 0,521 \\
\hline\( P_{2}(3,99 \mid 0,400592) \) & \( -40,0592 \) & \( 0,0592<0,1 \) \\
\hline\( P_{2}(3,999 \mid 0,0400060) \) & \( -40,0060 \) & \( 0,0060<0,1 \) \\
\hline\( P_{2}(4,1 \mid-3,9319) \) & \( -39,319 \) & 0,681 \\
\hline\( P_{2}(4,01 \mid-0,399392) \) & \( -39,9392 \) & \( 0,0608<0,1 \) \\
\hline\( P_{2}(4,001 \mid-0,0399940) \) & \( -39,9940 \) & \( 0,0060<0,1 \) \\
\hline
\end{tabular}
Problem/Ansatz:
Ich verstehe nicht wie ich mit dem Taschenrechner (Grafikrechner von Casio) auf die Sekantensteigung komme. Ich verstehe nicht, wie ich das machen muss.