Allgemeine Lösung Matrix

Question

Aufgabe:

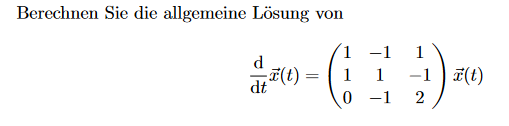
Text erkannt:

Berechnen Sie die allgemeine Lösung von
\( \frac{\mathrm{d}}{\mathrm{d} t} \vec{x}(t)=\left(\begin{array}{ccc} 1 & -1 & 1 \\ 1 & 1 & -1 \\ 0 & -1 & 2 \end{array}\right) \vec{x}(t) \)

Mein Ansatz ist wie folgt:

1) Die Eigenwerte bestimmen, da habe ich {2, -1+i, -1-i}.

2) Geometrische Vielfachheit Lambda mit der algebraischen von Lambda vergleichen

Weiteres habe ich nicht gefunden und im Skript aus meiner Uni ist das sehr komplex erklärt ohne Beschriftung der Schritte.

Wäre dankbar für eine Aufklärung :)

Answer 1

Hallo,

1) Die Eigenwerte bestimmen, da habe ich {2, -1+i, -1-i}.

ich habe 1 (doppelt) und 2 erhalten

Danach mußt Du die Eigenvektoren bestimmen und weil 1 doppelt ist , die Hauptwerte.

b)Eigenvektoren:

Ergebnis Wolfram Alpha:

Lösung:

\( x=c_{1} e^{2 t}\left(\begin{array}{l}1 \\ 0 \\ 1\end{array}\right)+c_{2} e^{t}\left(\begin{array}{l}1 \\ 1 \\ 1\end{array}\right)+c_{3} e^{t}\left(t\left(\begin{array}{l}1 \\ 1 \\ 1\end{array}\right)+\left(\begin{array}{c}1 \\ -1 \\ 0\end{array}\right)\right) \)