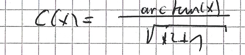Bestimmen Sie r(x) so, dass y(x) = arctan(x) eine Lösung der Differentialgleichung ist

Question

Wir betrachten die Differentialgleichung xy(x) = (x²+1)y′(x) + r(x) zu einer reellen Funktion r(x).

Bestimmen Sie r(x) so, dass y(x) = arctan(x) eine Lösung der Differentialgleichung ist und ermitteln Sie für das so
gewonnene r(x) eine Lösung dieser Differentialgleichung mit y(0) = 17!

Answer 1

Hallo,

y(x) =arctan(x)

y'(x)= \( \frac{1}{x^{2}+1} \)

einsetzen in :

xy(x) = (x^2+1)y′(x) + r(x)

-->r(x)= x arctan(x) -1

->Lösung durch Variation der Konstanten:

xy(x) = (x^2+1)y′(x) + x arctan(x)-1

->Lösung der hom. DGL:  xy(x) - (x^2+1)y′(x) =0

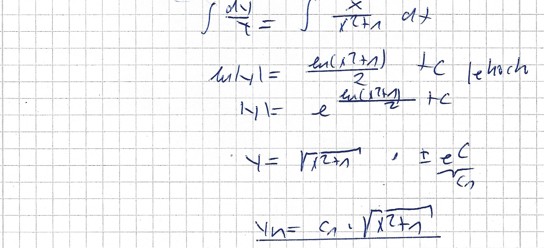
yh= C₁ *\( \sqrt{x^2 +1} \)

C1=C(x)

yp=C(x) *\( \sqrt{x^2 +1} \)

yp'= C'(x) *\( \sqrt{x^2 +1} \) +C(x) * \( \frac{x}{\sqrt{x^2 +1}} \)

yp und yp' in die DGL einsetzen:

zum Schluß die AWB in die Lösung einsetzen

Comments

Vielen lieben Dank!

---

Hallo, ich hab's mir jetzt nochmal genauer angeschaut und warum ist xy-(x²+1)y'=xarctan(x) und nicht xarctan(x)-1?

Man setzt doch die Ableitung y' ein und erhält xarctan(x)- (x²+1)* 1/(x²+1)

x²+1 kürzt sich raus und man erhält doch letztendlich xarctan(x)-1?

---

JA, Du hast Recht , ich habe korrigiert.

xy(x) = (x^2+1)y′(x) + r(x)