Aufgabe:
Guten Abend zusammen,
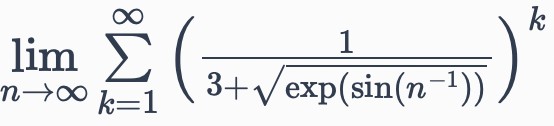
Text erkannt:
\( \lim \limits_{n \rightarrow \infty} \sum \limits_{k=1}^{\infty}\left(\frac{1}{3+\sqrt{\exp \left(\sin \left(n^{-1}\right)\right)}}\right)^{k} \)
Ich bin gerade dabei, den Grenzwert der folgenden Reihe zu bestimmen. Ich habe mir dazu einigen Gedanken gemacht:
Ich schaue mir zuerst den Ausdruck: \( \sqrt{exp(sin(n^-1))} \) an.
durch vereinfachen gilt: \( \sqrt{exp(sin(n^-1))} \) = \( \sqrt{exp(sin(1/n))} \)
Für n gegen unendlich geht der Term \( \frac{1}{n} \) gegen 0.
und sin(0) = 0
also gilt: \( \sqrt{exp(sin(n^-1))} \) = \( \sqrt{exp(0)} \) = \( \sqrt{e^0} \) = \( \sqrt{1} \) = 1 ??
Mein Gedanke:
Die Reihe\( \sum\limits_{k=1}^{\infty}{(\frac{1}{3+\sqrt{exp(sin(n^-1)}})^k} \) würde dann für n gegen unendlich gegen 4/3 konvergieren. Warum?
Wie eben gezeigt geht \( \sqrt{exp(sin(n^-1))} \) gegen 1 also gilt:
\( \sum\limits_{k=1}^{\infty}{(\frac{1}{3+1})^k} \)
Dies ist die geometrische Reihe, also kann man folgendes anwenden um den Grenzwert zu berechnen: (da q=1/4<1)
\( \frac{1}{1-\frac{1}{4}} \) = \( \frac{4}{3} \)
Für mich ergibt das alles sinn, aber es kann sein, dass ich einige generelle Rechenfehler habe bzw. meine Herangehensweise nicht korrekt ist.
Es wäre super lieb, wenn mir einer sagen könnte, ob das alles so sinn macht.
Vielen Dank!