Aufgabe:
f(t) = (1-2t) * sin(2t) ∈[0;π/2]
Bestimme die Extrema der Funktion f(t)
Problem/Ansatz:
Hallo, ich würde gerne wissen wie man die Extrema dieser Funktion bestimmt. Ich habe es schonmal versucht durchzurechnen, aber irgendwo muss mir ein Fehler unterlaufen sein, da mein Plot zu dem Ergebnis nicht stimmen kann.
f(t)' = -4*cos(2t) = 0
f(t)' = -4*cos(2t) = 0 / :(-4)
f(t)' = cos(2t) = 0 / arccos
f(t)' = 2t = arccos(0) + π/2n / :2
f(t)' = t = π/4 + π/4n | n = 0,1,2,3,4 ...
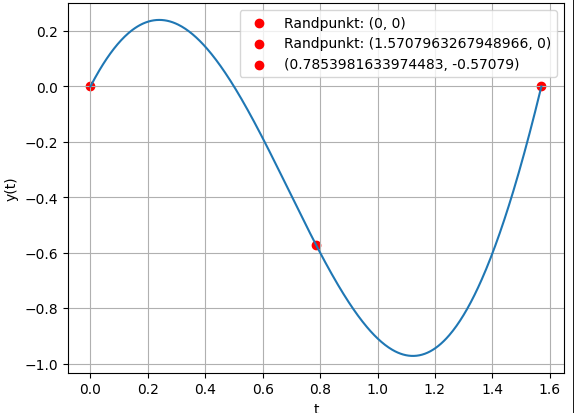
t1 = π/4
f(π/4) = -0.570796
Dann müsste eine Extrema bei (π/4/ -0.570796) liegen. Mein Plot sieht dann aber so aus:
Wo habe ich den Fehler gemacht? Ich komme nicht drauf. LG und danke im voraus.