Aufgabe:
Es sei X die Augenzahl bei einem einmaligen Wurf eines fairen 8-seitigen Würfels. Wie groß
ist die Wahrscheinlichkeit, dass die Augenzahl
a) größer als 4, b) nicht größer als 3, c) gleich 4 ist?
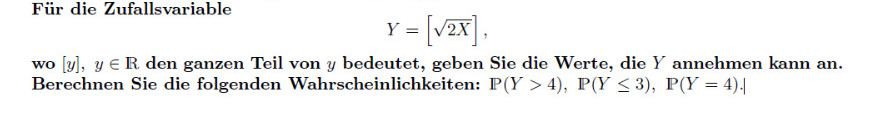
Problem/Ansatz:
Text erkannt:
Für die Zufallsvariable
\( Y=[\sqrt{2 X}], \)
wo \( [y], y \in \mathbb{R} \) den ganzen Teil von \( y \) bedeutet, geben Sie die Werte, die \( Y \) annehmen kann an. Berechnen Sie die folgenden Wahrscheinlichkeiten: \( \mathbb{P}(Y>4), \mathbb{P}(Y \leq 3), \mathbb{P}(Y=4) \).