Ich möchte näheres verstehen, ob die Gleichung unendliche viele Lösungen hat oder keine Lösung wie erkenne ich das …

Question

\( \begin{pmatrix} a & b \\ c & d \end{pmatrix} \) Aufgabe:

Gegeben ist folgendes Gleichungssystem:

1) d = a

2) 0,5a = b

3) 0,5b = c

4) 0,6c + 0,8d = d

Ich möchte näheres verstehen, ob die Gleichung unendliche viele Lösungen hat oder keine Lösung wie erkenne ich das beim Gauß verfahren?

Unendliche Lösungen -> Nullzeile am Ende

keine Lösung -> Ungleichheit

Ich habe am Ende folgende Matrix: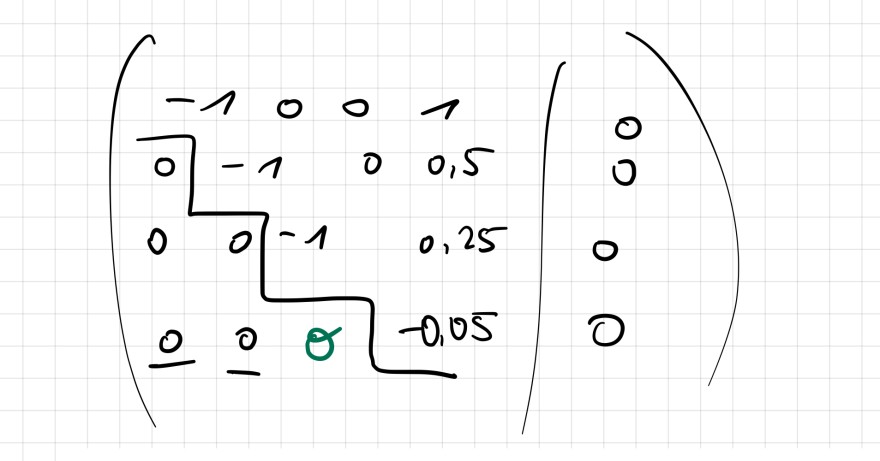

Text erkannt:

\( \left(\begin{array}{cccc|c}-1 & 0 & 0 & 1 & 0 \\ 0 & -1 & 0 & 0,5 & 0 \\ 0 & 0 & -1 & 0,25 & 0 \\ 0 & 0 & 0 & -0,05 & 0\end{array}\right) \)

Comments

Da steht schlußendlich -0,05 d=0

Was schießt Du daraus?

---

Ja das folglich d = 0 und somit b= a=c= d = 0 sind. Aber was ist das für eine Lösungsmenge? Eindeutige?

---

Homogene GLS haben entweder die triviale Lösung 0 (Vektor) oder unendlich viele Lösungen (dazu muß mind. eine Nullzeile (Gleichungen sind lin. abhängig)) nach Gauß entstehen).

Die Lösungsmenge besteht aus dem Nullvektor...

---

Bezogen auf Populationsmatrizen was hat eine triviale Lösung für eine bedeutung?

---

Populationsmatrizen ?

eine Population ohne Population?

---

ich dachte immer im Bezug auf LGS gubt es drei Möglichkeiten:

keine Lösung

unendlich

eindeutige

---

Na ja, Du hast eine eindeutige Lösung - wo ist das Problem?

Passt sie nicht zur Aufgabe?

Answer 1

Das Gleichungssystem lautet also

-a + d = 0
-b + 0.5·d = 0
-c + 0.25·d = 0
- 0.05·d = 0

Die letzte Gleichung sagt dir d = 0. Wenn du d = 0 einsetzt dann gilt auch nach den anderen Gleichungen a = b = c = 0

Das ist jetzt genau eine Lösung. Die letzte Zeile bestimmt immer wie viele Lösungen es gibt. Ist das so verständlich?

Auf folgender Seite findest du einen recht guten Merkzettel:

https://www.massmatics.de/merkzettel/#!337:Loesung_eines_Linearen_Gleichungssystems