Hinweis für Fortgeschrittene (keine Antwort für den Fragesteller):
Zwei Vektoren \(a\) und \(b\) in der Ebene spannen ein Parallelogramm auf, deren (vorzeichenbehafteter) Flächeninhalt \(F\) sich berechnet aus:$$F = a_xb_y - a_yb_x $$dies kann man auch als Vektorprodukt oder Determinante einer Matrix interpretieren:$$F=a \times b = \det\left(\left[\begin{array}{c} a_x&b_x\\ a_y& b_y \end{array}\right]\right) = a_xb_y - a_yb_x$$Im Fall der Gerade durch zwei Punkte \(A\) und \(B\), die gleichzeitig die Ortsvektoren zu den Punkten sind, kann man nun folgendes schließen:
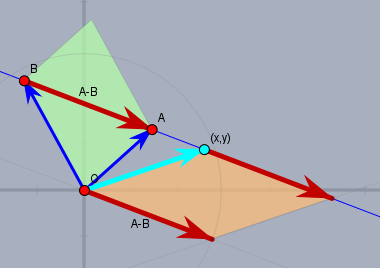
Die Ortsvektoren zu \(A\) und \(B\) (blau) spannen ein Parallelogramm (grün) auf, was aus zwei gleichen Dreicken mit der Grundseite \(|A-B|\) und der Höhe \(d\) besteht. \(d\) ist der Abstand der Gerade vom Ursprung \(O\). $$F_1 = 2\cdot \frac{|A-B|d}{2} = A \times B$$
Nun wähle man einen beliebigen Punkt \((x,y)\) auf der Geraden und betrachte den Vektor zu \((x,y)\) (hellblau) und den Differenzvektor \(A-B\) (rot). Diese Vektoren spannen ebenfalls ein Parallelogramm (orange) auf mit der Grundseite \(|A-B|\) und der Höhe \(d\).$$F_2 = |A-B| d = (A-B)\times \begin{pmatrix} x\\y \end{pmatrix}$$
Beide Flächen sind demnach gleich und daher gilt:$$(A-B) \times \begin{pmatrix} x\\y \end{pmatrix} = A \times B$$und fertig ist die Geradengleichung in Koordinatenform!
Im konkreten Fall mit den Punkten \(A\) und \(C\): $$\begin{aligned} (A-C)\times \begin{pmatrix} x\\y \end{pmatrix} &= A \times C \\ \left(\begin{pmatrix} -3\\5 \end{pmatrix}-\begin{pmatrix} 10\\-4 \end{pmatrix}\right) \times \begin{pmatrix} x\\y \end{pmatrix} &= \begin{pmatrix} -3\\5 \end{pmatrix}\times \begin{pmatrix} 10\\-4 \end{pmatrix}\\ \begin{pmatrix} -13\\9 \end{pmatrix} \times \begin{pmatrix} x\\y \end{pmatrix} &= -3\cdot(-4) - 5\cdot 10\\ -13y - 9x &= 12-50 \\9x+13y &= 38\\ \end{aligned}$$was nach Auflösen nach \(y\) natürlich zu der gleichen Lösung führt, die Silvia schon angegeben hat.