Wahrscheinlichkeitsrechnung Glücksrad drehen

Question

Aufgabe:

Bei einem Glücksrad mit fünf durchnummerierten Feldern beträgt die Wahrscheinlichkeit für die Zahl 5 30%, für die Zahl 1 10%, die Zahlen 2-4 erscheinen jeweils mit der gleichen Wahrscheinlichkeit.

Man vermutet, dass das Glücksrad seltener auf der 5 landet als angegeben. Diese Vermutung soll durch 100-maliges Drehen des Glücksrades getestet werden.
(i) Beschreiben Sie einen Hypothesentest zum Signifikanzniveau 5%, indem Sie den Annahmebereich aufstellen, den Test durchführen und die Ergebnisse interpretieren (den gefundenen Annahmebereich in Hinblick auf die Nullhypothese interpretieren)
(ii) Beschreiben Sie den Fehler 1. und 2.Art. Anschließend berechnen Sie den Fehler 1.Art und interpretieren Sie ihr Ergebnis.

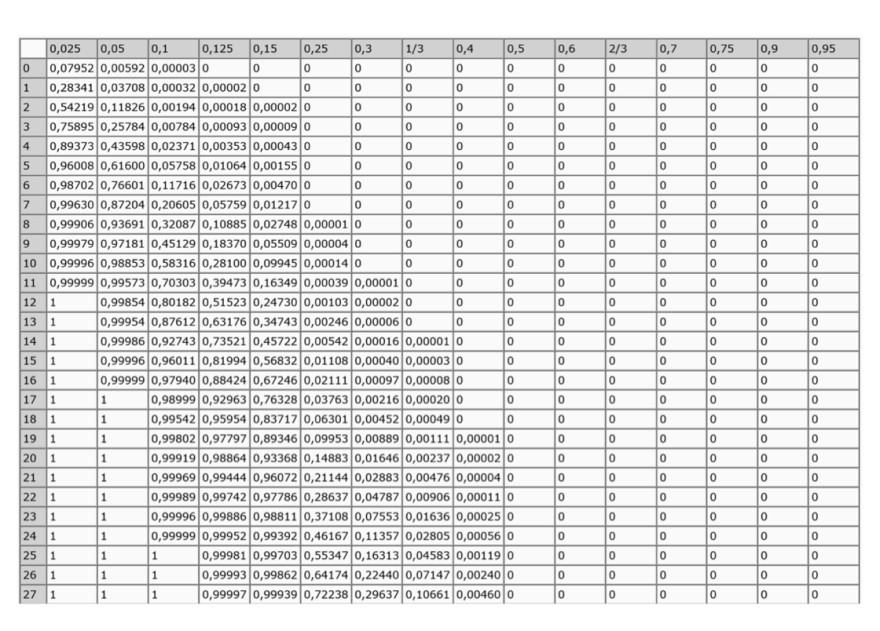
Ich habe bereits den Stichprobenumfang, das Signifikanzniveau, die Hypothesen (in Zeichen und in Worten) und die Art des Testes (links-, rechts- oder beidseitiger Test) festgelegt, weiß jetzt aber nicht was die Tabelle mir sagen soll und wie ich die oben aufgeführten Teile noch herausfinde.

Answer 1

Sei \(X\) binomialverteilt mit Parametern \(n=100\) und \(p\).

In der ersten Spalte steht, für welchen Wert von \(k\) die Zeile steht.

In der ersten Zeile steht, für welchen Wert von \(p\) die Spalte steht.

In den Zellen steht \(P(X\leq k)\).

seltener auf der 5 landet als angegeben.

\(H_0:\ p= 0.3\), \(H_1:\ p< 0.3\) also linksseitiger Test.

Die Nullhypothese wird also abgelehnt, wenn für das bei der Durchführung des Tests erzielte Ergebnis \(k\) gilt:

        \(P(X\leq k)\leq 0.05\).

Answer 2

Die Tabelle ist die kumulierte Verteilungsfunktion der Binomialverteilung für n = 100 und für verschiedene Werte von p. Interessant ist hier nur die Spalte für p = 0.3.

Die Nullhypothese (p >= 0.3) kann im Intervall [23 ; 100] nicht abgelehnt werden. Im Intervall [0 ; 22] würden wir die Nullhypothese ablehnen und tatsächlich vermuten, dass die 5 tatsächlich eine niedrigere Wahrscheinlichkeit besitzt.

Comments

Vielen Dank, ich kam deutlich weiter. Allerdings weiß ich jetzt final nur noch nicht wie ich auf den Fehler 2. Art komme.