Aufgabe:
Überprüfe ob folgende Matrize bezüglich der Multiplikation inverse ist
Problem/Ansatz:
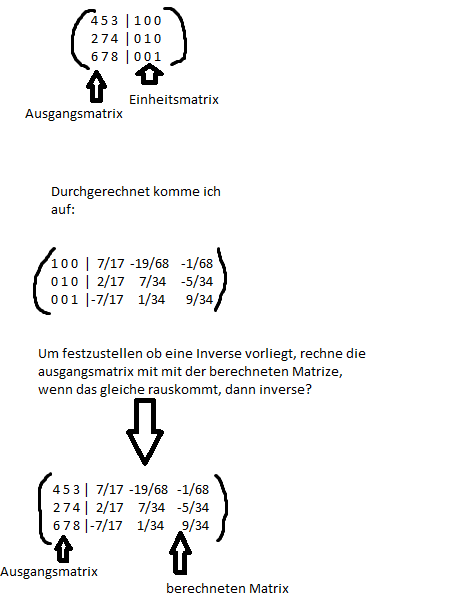
Text erkannt:
Durchgerechnet komme ich auf:
Um festzustellen ob eine Inverse vorliegt, rechne die ausgangsmatrix mit mit der berechneten Matrize, wenn das gleiche rauskommt, dann inverse?
\( \left(\begin{array}{rrrr} 453 & 7 / 17 & -19 / 68 & -1 / 68 \\ 274 & 2 / 17 & 7 / 34 & -5 / 34 \\ 678 & -7 / 17 & 1 / 34 & 9 / 34 \\ \text { ( } & & \end{array}\right) \)
Ausgangsmatrix
berechneten Matrix
Ich bin mir unsicher beim weiteren vorgehen. Um jetzt festzustellen, ob die Matrix inverse ist, muss ich die Ausgangsmatrix mit der berechneten Matrix multiplizieren(wie in der Abbildung angzeigt) , bis ich wieder eine Einheitsmatrix habe oder was soll ich nun tun?