Aufgabe:
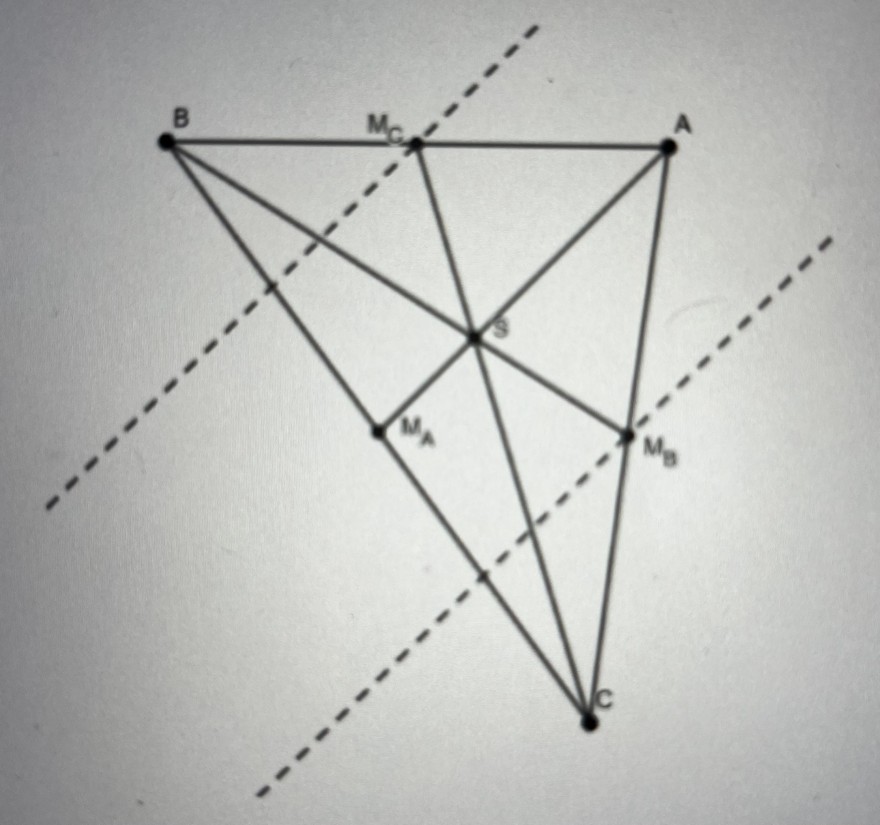
Die drei Seitenhalbierenden eines beliebigen Dreiecks schneiden sich in einem Punkt. Diesen Punkt nennt man den Schwerpunkt des Dreiecks. Es gilt die folgende Aussage: Der Schwerpunkt teilt alle Seitenhalbierenden in einem Verhältnis von 1/2 "
Beweisen Sie die Aussage für die Seitenhalbierende S_{B} Benutzen Sie dazu die gestrichelten Hilfsgeraden durch M_{B} und M_{c} parallel zur Seitenhalbierende S_{A} und mehrmals den ersten Strahlensatz.
Problem/Ansatz:
Hat jemand eine Idee, wie man diese Aufgabe lösen könnte?