Bestimmen Sie eine Iterationsformel x_{n+1}=I(x_{n}) zur Bestimmung einer Dezimaldarstellung der Zahl √{8} .

Question

Aufgabe:

Bestimmen Sie eine Iterationsformel \( x_{n+1}=I\left(x_{n}\right) \) zur Bestimmung einer Dezimaldarstellung der Zahl \( \sqrt{8} \).

Problem/Ansatz:

Wie geht das? Danke im voraus

Answer 1

Aloha :)

Wir suchen die Zahl \((x=\sqrt8)\). Dann muss \((x^2=8)\) gelten oder auch \(\pink{x=\frac8x}\).

Wegen \(3^2=9\) beginnen wir die Iteration mit dem ersten Schätzwert \(x_1=3\).

Bei der Berechung der Iterationsfolge \((x_n)\) wollen wir erreichen, dass sich die Werte \(\pink{x_n}\) und \(\pink{\frac{8}{x_n}}\) immer weiter aufeinander zu bewegen, bis sie nach unendlich vielen Schritten schließlich gleich werden und wir damit \(x_\infty=\sqrt8\) erhalten.

Daher nehmen wir den Mittelwert dieser beiden Werte als neuen Schätzwert für das nächste Folgenglied \(x_{n+1}\). Denn der Mittelwert liegt immer zwischen \(x_n\) und \(\frac{8}{x_n}\) und sollte daher in jedem Schritt eine bessere Näherung ergeben. Formal heißt das:$$x_{n+1}=\frac{x_n+\frac{8}{x_n}}{2}\quad;\quad x_1=3$$

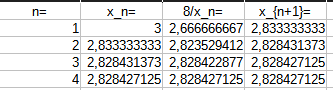
Bereits nach 4 Schritten ändert sich das Ergebnis mit 10 Stellen Genauigkeit nicht mehr:

Comments

Dankeschön, jetzt verstehe ich es auch.