Newton-Verfahren: Nullstelle und Quadratwurzlel

Question

Berechnen sie mit Hilfe des Newton-Verfahrens die Nullstelle der Funktion f so genau, wie es ihr Taschenrechner vermag.

$$ f(x) = x^3 + x + 1 $$

Bestimmen Sie die Quadratwurzel \( x = \sqrt{5} \) Hilfe des Newtonverfahrens.

Answer 1

Das Newton-Verfahren zur numerischen Bestimmung einer Nullstelle einer Funktion  f  lautet

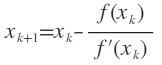
Ist  f(x) = x³ + x + 1, so ist f'(x) = 3x² + 1. Dann lautet die Rekursion

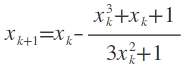
oder etwas zusammengefasst

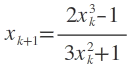
Starte z.B. mit x₀ = 0. Die Rekursion ergibt mit meinem TR nach 5 Schritten

x₅ = -0.6823278.

Danach gibt es keine Änderung mehr.

 

Zum zweiten Teil setze f(x) = x² - 5. Dann ist f'(x) = 2x. Wähle z.B. x₀ = 2 und verfahre wie beschrieben.