Aufgabe:
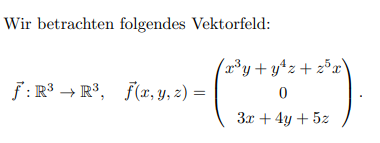
Text erkannt:
Wir betrachten folgendes Vektorfeld:
\( \vec{f}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}, \quad \vec{f}(x, y, z)=\left(\begin{array}{c} x^{3} y+y^{4} z+z^{5} x \\ 0 \\ 3 x+4 y+5 z \end{array}\right) \)

Text erkannt:
Bestimmen Sie grad div \( \vec{f} \).
Bestimmen Sie rot rot \( \vec{f} \)
Hinweis: Benutzen Sie die allgemeine Identität
\( \Delta \vec{u}=\operatorname{grad} \operatorname{div} \vec{u}-\operatorname{rot} \operatorname{rot} \vec{u} \)
für zweimal stetig partiell differenzierbare Vektorfelder \( \vec{u}: G \subset \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}\left(G \subset \mathbb{R}^{3}\right. \) offen).
Problem/Ansatz: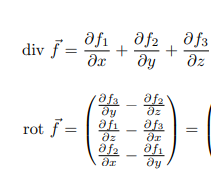 wie muss man vorgehen wenn die aufgaben wie oben sind.
wie muss man vorgehen wenn die aufgaben wie oben sind.
muss man bei der ersten aufgabe zuerst den grad aufstellen und dann div f?
Bei rot rot 2 mal ? Kann einer schritt für schritt mit erklärung mir die aufgabe zeigen
Text erkannt:
\( \begin{aligned} \operatorname{div} \vec{f}= & \frac{\partial f_{1}}{\partial x}+\frac{\partial f_{2}}{\partial y}+\frac{\partial f_{3}}{\partial z} \\ \operatorname{rot} \vec{f}= & \left(\begin{array}{l}\frac{\partial f_{3}}{\partial y}-\frac{\partial f_{2}}{\partial z} \\ \frac{\partial f_{1}}{\partial z}-\frac{\partial f_{3}}{\partial x} \\ \frac{\partial f_{2}}{\partial x}-\frac{\partial f_{1}}{\partial y}\end{array}\right)=\end{aligned} \)