Aufgabe:
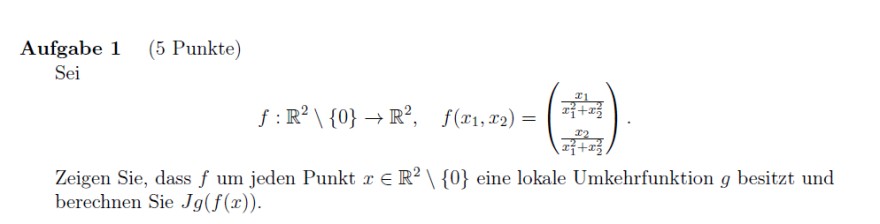
Text erkannt:
\( \begin{array}{l} \text { Aufgabe } 1 \text { (5 Punkte) } \\ \qquad \begin{array}{l} \text { Sei } \end{array} \\ \qquad f: \mathbb{R}^{2} \backslash\{0\} \rightarrow \mathbb{R}^{2}, \quad f\left(x_{1}, x_{2}\right)=\left(\begin{array}{c} \frac{x_{1}}{x_{1}^{2}+x_{2}^{2}} \\ \frac{x_{2}}{x_{1}^{2}+x_{2}^{2}} \end{array}\right) . \end{array} \)
Zeigen Sie, dass \( f \) um jeden Punkt \( x \in \mathbb{R}^{2} \backslash\{0\} \) eine lokale Umkehrfunktion \( g \) besitzt und berechnen Sie \( J g(f(x)) \).