Zeigen Sie, dass sich F=0 nahe (0,0,0,0) lokal nach (u, v) aufösen lässt, dass es also in einer offenen Umgebung U …

Question

Aufgabe:

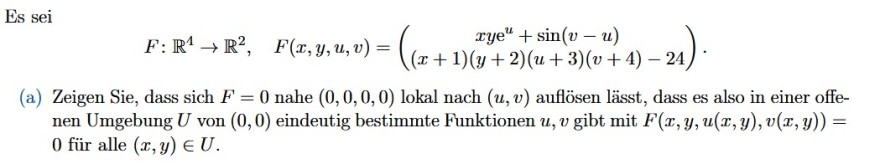
Text erkannt:

Es sei
$F: \mathbb{R}^{4} \rightarrow \mathbb{R}^{2}, \quad F(x, y, u, v)=\left(\begin{array}{c} x y \mathrm{e}^{u}+\sin (v-u) \\ (x+1)(y+2)(u+3)(v+4)-24 \end{array}\right)$
(a) Zeigen Sie, dass sich $F=0$ nahe $(0,0,0,0)$ lokal nach $(u, v)$ aufösen lässt, dass es also in einer offenen Umgebung $U$ von $(0,0)$ eindeutig bestimmte Funktionen $u, v$ gibt mit $F(x, y, u(x, y), v(x, y))=$ 0 für alle $(x, y) \in U$.

Problem/Ansatz:

Ich bin mir hier überhaupt nicht sicher, welchen Satz ich hier anwenden soll. Eigentlich kann man hier doch sicher was rechnen, aber ich weiß leider nicht wo ich anfangen soll

Comments

Im anderen Forum hast du doch richtige Ansätze?https://matheplanet.de

---

ja die hatte ich erst heute hinbekommen. Aber weil hier keiner geantwortet hat habe ich sie da noch gestellt

---

Hallo

geantwortet wurde hier doch durch deine Kollegin?

lul

Answer 1

Hallo

die Antwort hat ne Kollegin von dir hier:https://www.mathelounge.de/1023344/die-gleichung-kann-danach-einer-u…