Aufgabe:
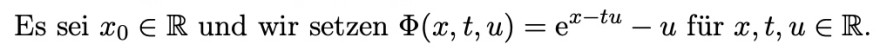
Text erkannt:
Es sei \( x_{0} \in \mathbb{R} \) und wir setzen \( \Phi(x, t, u)=\mathrm{e}^{x-t u}-u \) für \( x, t, u \in \mathbb{R} \).

Text erkannt:
Zeigen Sie, dass die Gleichung \( \Phi(x, t, u)=0 \) in einer Umgebung von \( \left(x_{0}, 0, \mathrm{e}^{x_{0}}\right) \) differenzierbar nach \( u \) auflösbar ist, es also eine offene Umgebung \( V \) von \( (x, t) \) und eine eindeutig bestimmte differenzierbare Funktion \( u: V \rightarrow \mathbb{R} \) gibt mit \( \Phi(x, t, u(x, t))=0 \) für \( (x, t) \in V \).
Problem/Ansatz:
Wir müssen zeigen, dass die Gleichung Φ(x, t, u) = 0 in einer Umgebung von (x0, 0, e^x0) differenzierbar nach u auflösbar ist und die partielle Ableitung ∂Φ/∂u betrachten und zeigen, dass sie in einer geeigneten Umgebung existiert. Die partielle Ableitung ∂Φ/∂u = -te^(x-tu) - 1 ist eine stetige Funktion in V. Da die partielle Ableitung ∂Φ/∂u in der Umgebung V = U × T von (x0, 0, e^x0) stetig ist, erfüllt sie die Voraussetzungen, um die Existenz und Eindeutigkeit einer differenzierbaren Funktion u: V → R zu gewährleisten, die die Gleichung Φ(x, t, u(x, t)) = 0 erfüllt ? Wir sind uns bei allem unsicher und wir wissen nicht mehr weiter