Diskrete Verteilung, Erwartungswert und Empirie

Question

Aufgabe: Sie wissen, dass für die diskrete Verteilung der Ergebnisse X∈{1,2,3,4,5,6}
eines gezinkten Würfels die folgende Wahrscheinlichkeitsfunktion herangezogen werden kann:

g für Augenzahl x=1

0,10 für Augenzahl x=2

0,16 für Augenzahl x=3

0,13 für Augenzahl x=4

0,34 für Augenzahl x=5

0,14 für Augenzahl x=6

1. Bestimmen Sie den Wert von g
so, dass es sich bei fX(x)
um eine Wahrscheinlichkeitsverteilung handelt: g=

2. Berechnen Sie den Erwartungswert E(X)=

In der nachfolgenden Tabelle sind die empirischen Ergebnisse des Würfelns mit einem Würfel enthalten. Sie wissen allerdings nicht, ob es sich dabei um den gezinkten Würfel handelt oder nicht.

Insgesamt wurde n=80 mal gewürfelt und die folgenden Häufigkeiten ni bzw. hi ermittelt:

Text erkannt:

Index $i \quad$ Augenzahl $x_{i} \quad$ Anzahl $n_{i} \quad$ rel. Häufigkeit $h_{i}$
\begin{tabular}{cccc}
1 & 1 & 9 & 0.1125 \\
\hline 2 & 2 & 12 & 0.1500 \\
\hline 3 & 3 & 11 & 0.1375 \\
\hline 5 & 4 & 8 & 0.1000 \\
\hline 6 & 6 & 23 & 0.2875 \\
\hline 4 & 17 & 0.2125
\end{tabular}
3. Berechnen Sie für die empirischen Ergebnisse den Mittelwert $\bar{x}$ aller 80 gewürfelten Augenzahlen $x_{i}$, die
Standardabweichung $s_{x}$ und den Standardfehler des
Mittelwert (se = standard error) $s e_{x}=\frac{s_{x}}{\sqrt{n}}$.
Folgende Zwischenergebnisse dürften hierbei hilfreich sein:
$\begin{array}{l} \sum \limits_{i=1}^{80} x_{i}=\sum \limits_{i=1}^{6} n_{i} x_{i}=315 \\ \circ \sum \limits_{i=1}^{80} x_{i}^{2}=\sum \limits_{i=1}^{6} n_{i} x_{i}^{2}=1471 \\ \text { Mittelwert } \bar{x}= \end{array}$
Mittelwert $\bar{x}=$
Standard-Abweichung $s_{x}=$
Standardfehler des Mittelwerts: $s e_{x}=$
4. Ermitteln Sie nun basierend auf den Ergebnissen der vorherigen Teilaufgabe das 95\%-Konfidenzintervall (KI) des Mittelwerts gemäß
$K I_{95 \%}=[U ; O]=\left[\bar{x}-2 s e_{x} ; \bar{x}+2 s e_{x}\right]$ :
Untergrenze $U=$
obergrenze $U=$

Text erkannt:

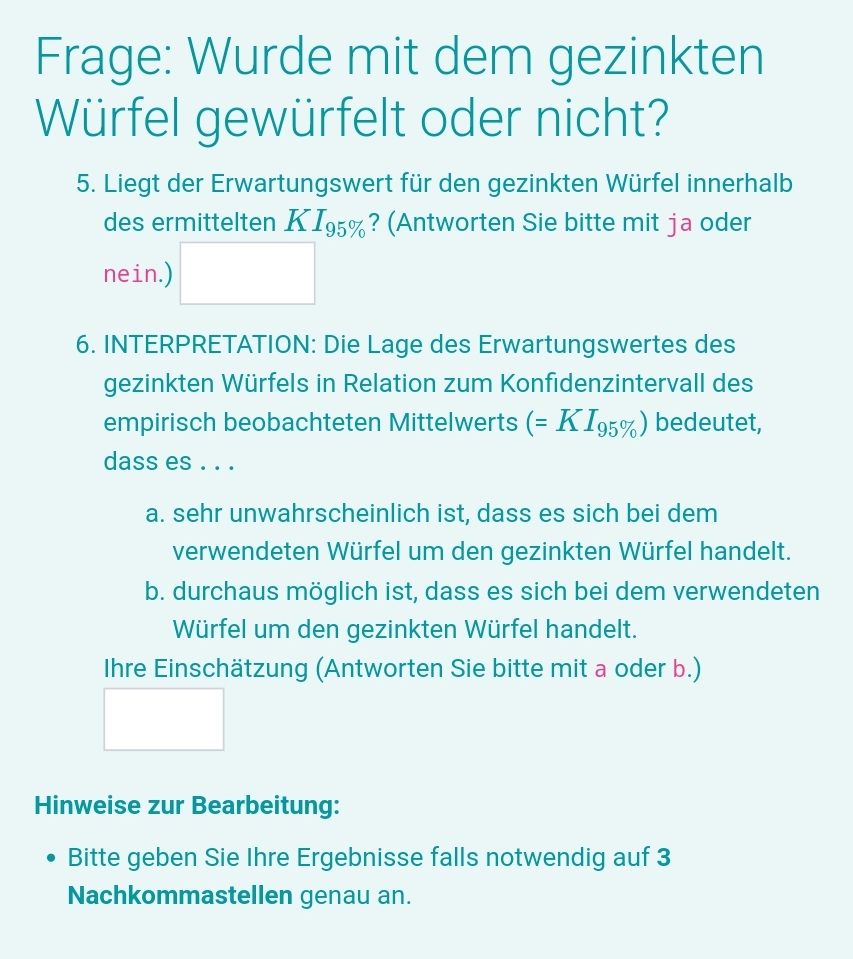
Frage: Wurde mit dem gezinkten Würfel gewürfelt oder nicht?
5. Liegt der Erwartungswert für den gezinkten Würfel innerhalb des ermittelten $K I_{95 \%}$ ? (Antworten Sie bitte mit ja oder nein.)
6. INTERPRETATION: Die Lage des Erwartungswertes des gezinkten Würfels in Relation zum Konfidenzintervall des empirisch beobachteten Mittelwerts $\left(=K I_{95 \%}\right.$ ) bedeutet, dass es ...
a. sehr unwahrscheinlich ist, dass es sich bei dem verwendeten Würfel um den gezinkten Würfel handelt.
b. durchaus möglich ist, dass es sich bei dem verwendeten Würfel um den gezinkten Würfel handelt.
Ihre Einschätzung (Antworten Sie bitte mit a oder b.)
Hinweise zur Bearbeitung:
- Bitte geben Sie Ihre Ergebnisse falls notwendig auf 3 Nachkommastellen genau an.

Es ist mein letzter Versuch und ich komme nur auf falsche Ergebnisse. Ich wäre für jede Antwort dankbar. Natürlich wird die hilfreichste Antwort ausgezeichnet.

Comments

Also 1 und 2 hast du auch nicht korrekt?

---

Das weiß ich nicht weil bei jedem Versuch die Zahlen anders sind :(

---

Hallo

erläutere lieber dein Vorgehen, damit wir deinen Fehler finden. z.B ist für die Zahlen g=0,13

Gruß lul