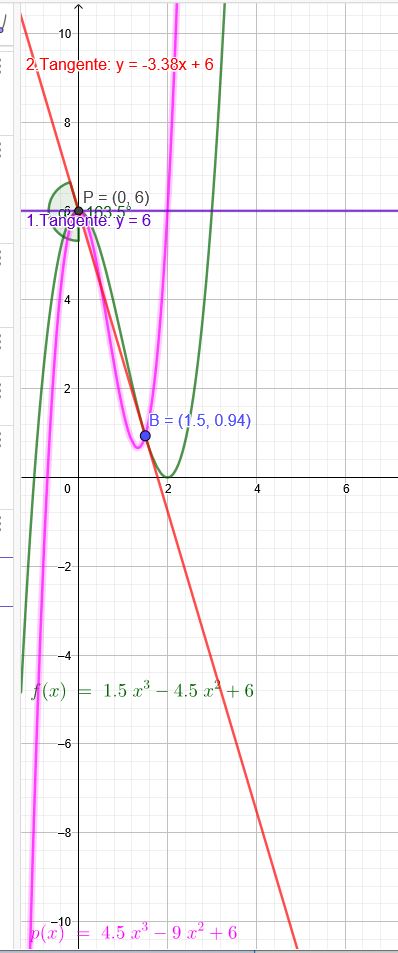
\(f(x) = 1,5x^3-4,5x^2+6\)
\(f´(x) = 4,5x^2-9x\)
\(P(0|6)\)
\( \frac{y-6}{x}=4,5x^2-9x \)
\( y=4,5x^3-9x^2+6 \)
\( 4,5x^3-9x^2+6=1,5x^3-4,5x^2+6 \)
\( 3x^3-4,5x^2=0 \)
\( x^2*(3x-4,5)=0 \)
\( x_1=0 \) \( y_1=6 \) → \(f´(0) = 0\) → Winkel mit y-Achse \(0°\)
\( x_2=1,5 \) \( y_2=1,5*1,5^3-4,5*1,5^2+6=\frac{15}{16} \) → \(f´(1,5) = 4,5*1,5^2-9*1,5\\= 4,5*1,5^2-9*1,5=-\frac{27}{8}\) → Winkel mit y-Achse \(16,5°\)