Zeigen Sie: Ist \varphi:(-r, r) → ℝ(r 0) eine Lösung der DGL y^{\prime}=f(x, y) , dann ist \varphi(x)=\varphi(-x) …

Question

Aufgabe:

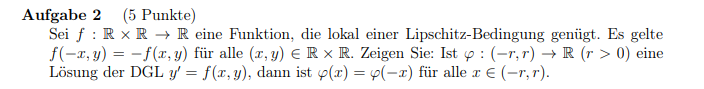
Text erkannt:

Aufgabe 2 (5 Punkte)
Sei \( f: \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R} \) eine Funktion, die lokal einer Lipschitz-Bedingung genügt. Es gelte \( f(-x, y)=-f(x, y) \) für alle \( (x, y) \in \mathbb{R} \times \mathbb{R} \). Zeigen Sie: Ist \( \varphi:(-r, r) \rightarrow \mathbb{R}(r>0) \) eine Lösung der DGL \( y^{\prime}=f(x, y) \), dann ist \( \varphi(x)=\varphi(-x) \) für alle \( x \in(-r, r) \).

Ich weiß nicht wie ich hier vorgehen muss

Answer 1

Es sei

$$\psi:(-r,r) \to \R, \quad \psi(x):=\phi(-x)$$

Dann ist \(\psi(0)=\phi(0)\) und

$$\psi'(x)=-\phi'(-x)=-f(-x,\phi(-x))=f(x,\phi(-x))=f(x;\psi(x))$$

Also löst \(\psi\) dasselbe Anfangswertproblem wie \(\phi\). Wegen der Eindeutigkeit der Lösung des AWP ist \(\psi=\phi\).